異常検知①

最終更新 2020-01-29 読了時間 2 分

まとめ

ADTKの基本検出器（閾値・統計ベース）を使い、時系列の異常をルールベースで検出する。rn- 特徴量設計と検出器選択の組み合わせで、誤検知と見逃しのバランスを調整する。rn- 検知結果の可視化により、異常判定の妥当性を運用目線で確認できる。

直感 #

ADTKは「モデルを1つ学習して終わり」ではなく、時系列の特徴量変換と検出器を部品として組み合わせる発想です。対象データの周期性や変動幅に合わせて検出ロジックを構成することで、運用しやすい異常検知パイプラインを作れます。

詳細な解説 #

1. 実験データの準備 #

ここでは Numenta Anomaly Benchmark (NAB) のデータを使い、
ADTK (Anomaly Detection Toolkit) で異常検知を試します。

1
2
3
4
5
6
7
8
import pandas as pd
from adtk.data import validate_series

s_train = pd.read_csv(
    "./training.csv", index_col="timestamp", parse_dates=True, squeeze=True
)
s_train = validate_series(s_train)
print(s_train.head())

1
2
from adtk.visualization import plot
plot(s_train)

2. 代表的な異常検知手法 #

ADTKには様々な検出器が用意されています。ここでは代表的な5種類を比較します。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
from adtk.detector import (
    AutoregressionAD,
    InterQuartileRangeAD,
    LevelShiftAD,
    PersistAD,
    SeasonalAD,
)

model_dict = {
    "LevelShiftAD": LevelShiftAD(window=5),
    "SeasonalAD": SeasonalAD(),
    "PersistAD": PersistAD(c=3.0, side="positive"),
    "InterQuartileRangeAD": InterQuartileRangeAD(c=1.5),
    "AutoregressionAD": AutoregressionAD(n_steps=14, step_size=24, c=3.0),
}

for model_name, model in model_dict.items():
    anomalies = model.fit_detect(s_train)
    plot(s_train, anomaly=anomalies, anomaly_color="red", anomaly_tag="marker")
    plt.title(model_name)
    plt.show()

3. 各手法の直感と数式 #

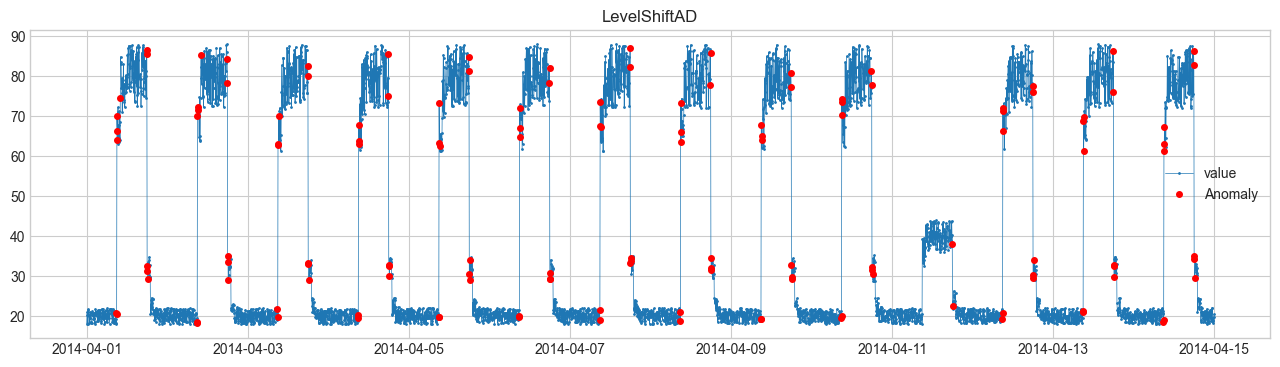
(1) LevelShiftAD（水準の変化） #

データの平均値が急に変化するかどうかを見る。
例：センサー値がある時点で急に上がった/下がった。

$$ \Delta_t = \bar{x}_{t:t+w} - \bar{x}_{t-w:t} $$

もし $|\Delta_t|$ が大きければ異常と判定。

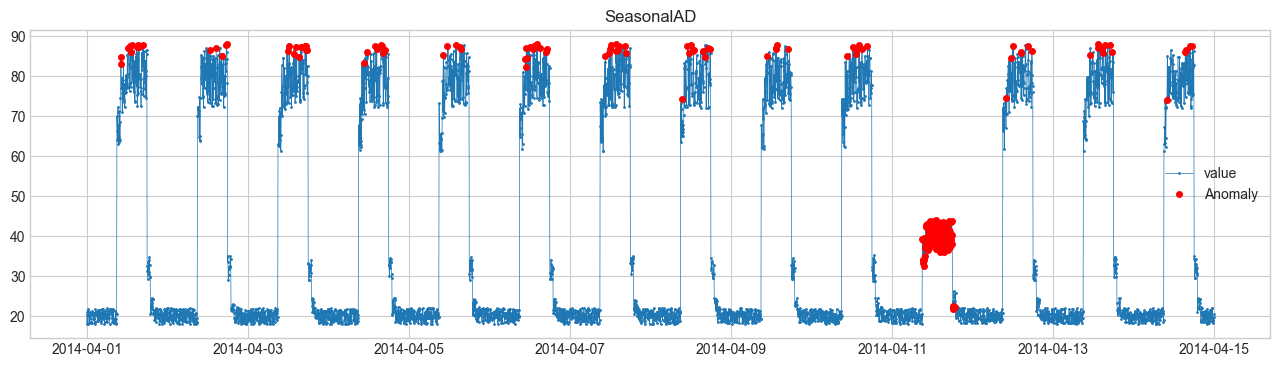
(2) SeasonalAD（季節性とのズレ） #

周期性を学習し、そのパターンから外れるデータを検知。
例：毎日のアクセス数が急に増えすぎた。

$$ e_t = x_t - \hat{x}_t^{(\text{seasonal})} $$

誤差 $e_t$ が大きければ異常。

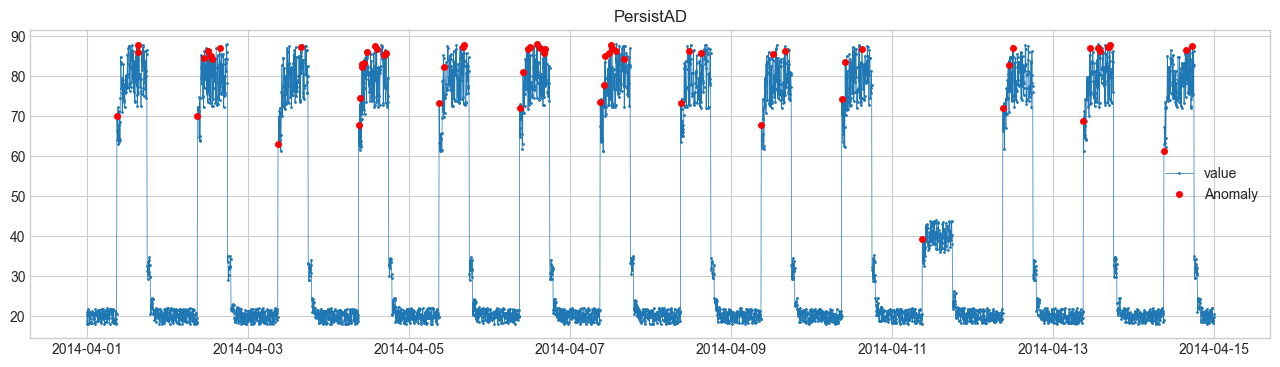
(3) PersistAD（値の持続） #

「過去の値から大きく乖離したか」を判定。

$$ |x_t - x_{t-1}| > c \cdot \sigma $$

閾値 $c$ を超えると異常。

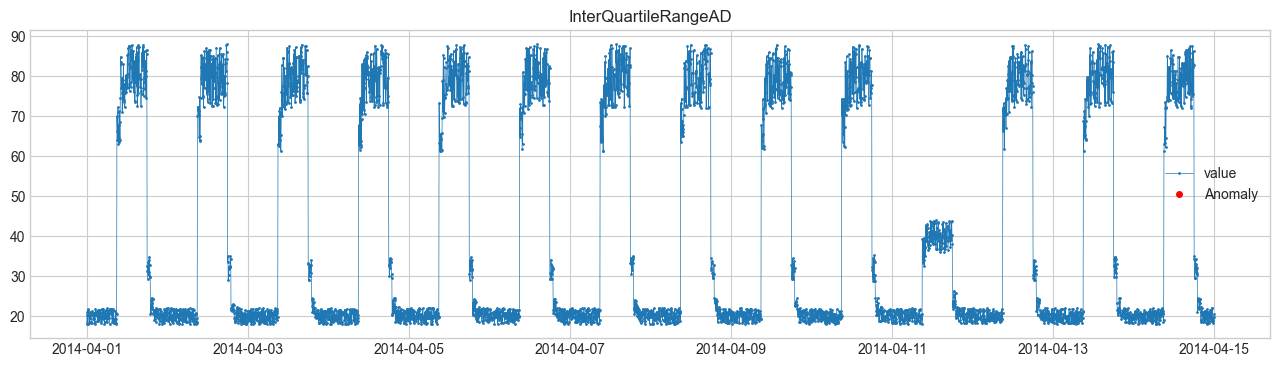
(4) InterQuartileRangeAD（四分位範囲） #

統計的に外れ値を検出。
データ分布の第1四分位 $Q1$、第3四分位 $Q3$、四分位範囲 $IQR=Q3-Q1$ を用いる。

$$ x_t < Q1 - c \cdot IQR \quad \text{または} \quad x_t > Q3 + c \cdot IQR $$

(5) AutoregressionAD（自己回帰） #

過去の値から未来を予測し、誤差が大きい点を異常とする。

$$ x_t \approx \sum_{i=1}^p \phi_i x_{t-i} + \epsilon_t $$

残差 $\epsilon_t$ が大きいと異常。

4. 可視化結果 #

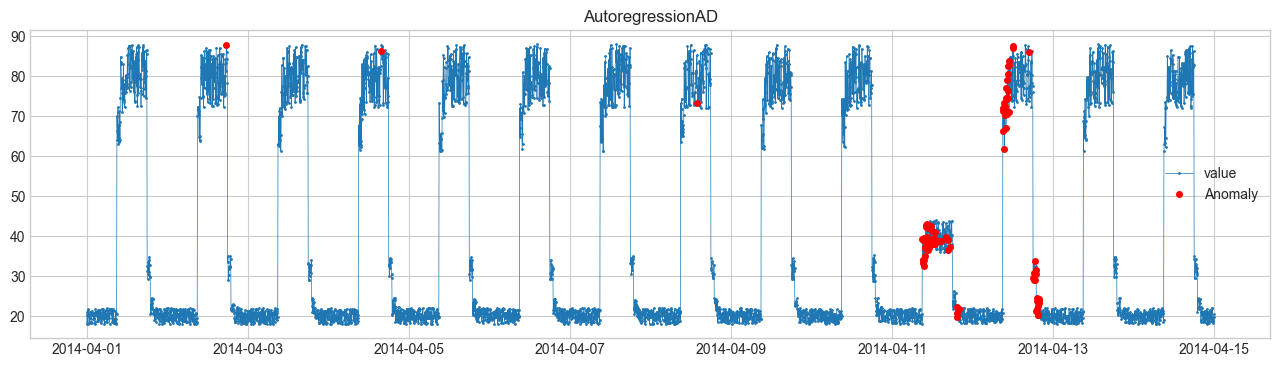
可視化結果

異常検知② — 続編
Isolation Forest — ツリーベースの異常検知
One-Class SVM — SVMベースの異常検知手法