異常検知②

最終更新 2026-02-16 読了時間 1 分

まとめ

ADTK応用編では、ウィンドウ処理や季節性を使った検出器で複雑な異常パターンを扱う。rn- 複数検出器の組み合わせにより、単一ルールでは難しい異常を捉えられる。rn- 検知結果を時系列上で比較し、業務要件に合う検出ロジックへ改善できる。

直感 #

adtk2のポイントは、時間窓や周期性を取り込んで「文脈付き」で異常を判定することです。同じ値でも時間帯や季節で意味が変わるケースを、検出器の組み合わせで表現します。

詳細な解説 #

Anomaly Detection Toolkit (ADTK)を使った異常検知をしてみます。多次元の人工データに対して異常検知を適用します。今度は複数次元のデータに対して異常検知を適用します。

import numpy as np
import pandas as pd
from adtk.data import validate_series

s_train = pd.read_csv("./training.csv", index_col="timestamp", parse_dates=True)
s_train = validate_series(s_train)
s_train["value2"] = s_train["value"].apply(lambda v: np.sin(v) + np.cos(v))
s_train

	value	value2
timestamp
2014-04-01 00:00:00	18.090486	0.037230
2014-04-01 00:05:00	20.359843	1.058643
2014-04-01 00:10:00	21.105470	0.141581
2014-04-01 00:15:00	21.151585	0.076564
2014-04-01 00:20:00	18.137141	0.103122
...	...	...
2014-04-14 23:35:00	18.269290	0.288071
2014-04-14 23:40:00	19.087351	1.207420
2014-04-14 23:45:00	19.594689	1.413067
2014-04-14 23:50:00	19.767817	1.401750
2014-04-14 23:55:00	20.479156	0.939501

4032 rows × 2 columns

from adtk.visualization import plot

plot(s_train)

png

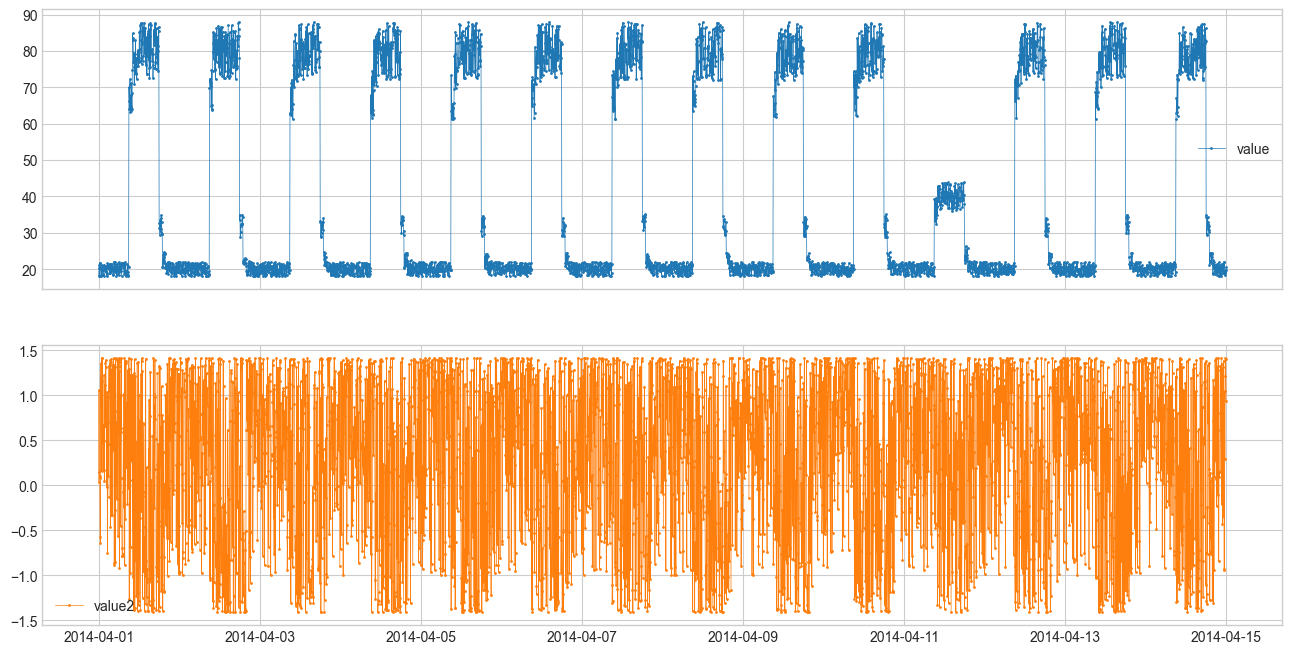
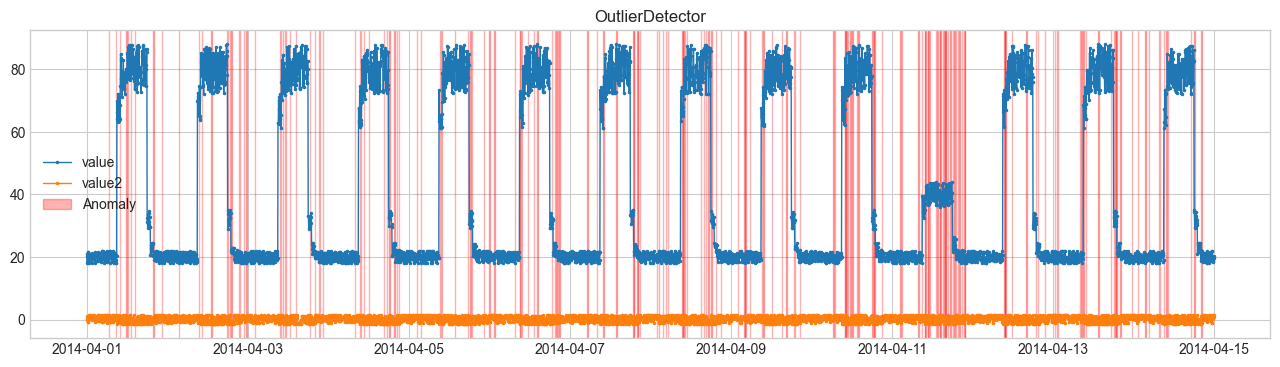
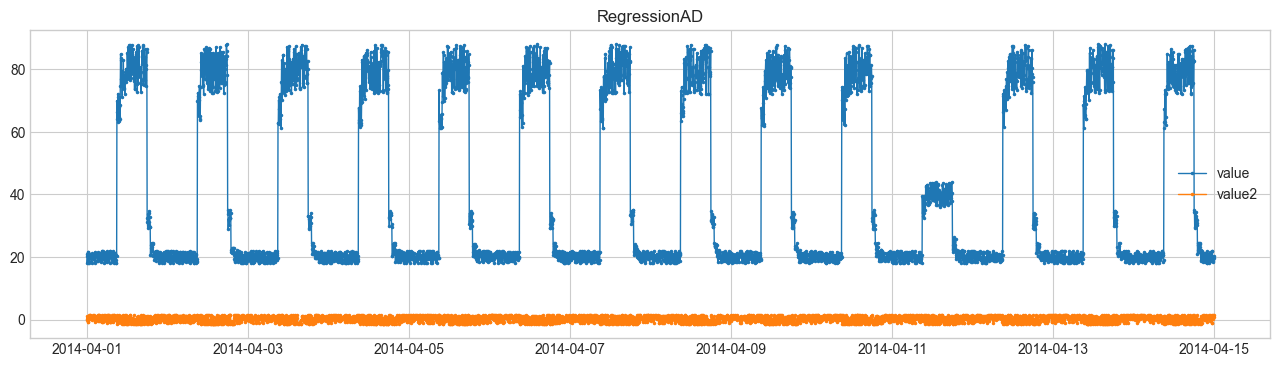
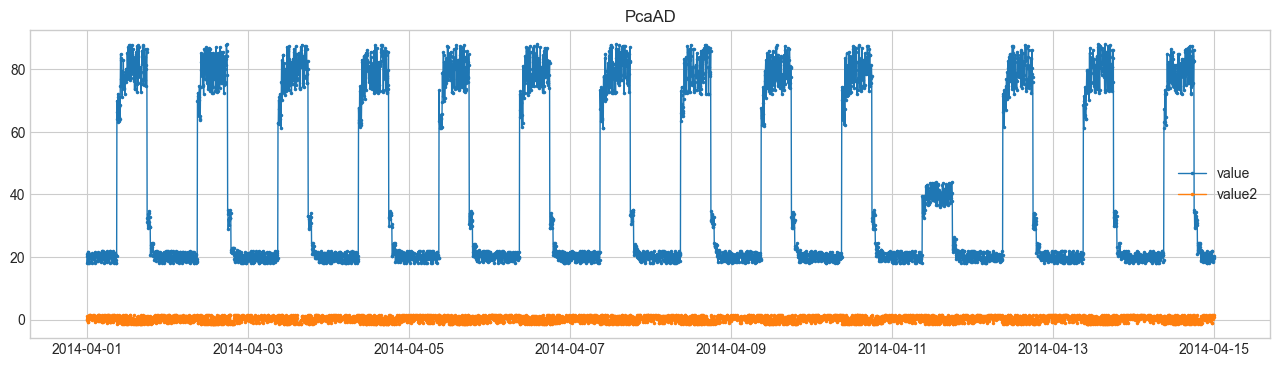
異常検知手法の比較 #

SeasonalADを用いた異常検知を行います。他の手法はDetectorを参照してください。

import matplotlib.pyplot as plt
from adtk.detector import OutlierDetector, PcaAD, RegressionAD
from sklearn.linear_model import LinearRegression
from sklearn.neighbors import LocalOutlierFactor

model_dict = {
    "OutlierDetector": OutlierDetector(LocalOutlierFactor(contamination=0.05)),
    "RegressionAD": RegressionAD(regressor=LinearRegression(), target="value2", c=3.0),
    "PcaAD": PcaAD(k=2),
}

for model_name, model in model_dict.items():
    anomalies = model.fit_detect(s_train)

    plot(
        s_train,
        anomaly=anomalies,
        ts_linewidth=1,
        ts_markersize=3,
        anomaly_color="red",
        anomaly_alpha=0.3,
        curve_group="all",
    )
    plt.title(model_name)
    plt.show()

png