サポートベクターマシン (SVM)

中級

2.2.5

サポートベクターマシン (SVM)

最終更新 2020-03-25 読了時間 4 分
まとめ
  • SVM はクラス間のマージンを最大化する決定境界を学習し、汎化性能を重視した分類器を構築します。
  • ソフトマージンではスラック変数を導入して誤分類を許容し、罰則係数 \(C\) でマージン幅とのバランスを制御します。
  • カーネルトリックを使えば内積をカーネル関数に置き換え、明示的に特徴量を増やさなくても非線形境界を扱えます。
  • 前処理としての標準化と、\(C\) や \(\gamma\) といったハイパーパラメータ探索が性能向上の鍵になります。

直感 #

分離超平面が複数存在するとき、SVM はサンプルから最も離れたマージンが最大のものを選びます。マージンに接するサンプルはサポートベクターと呼ばれ、彼らだけが最終的な境界を決定します。その結果、多少のノイズに強い滑らかな決定境界になります。

flowchart LR A["入力データ"] --> B["特徴空間へ写像\nカーネルトリック"] B --> C["マージン最大化\n超平面を探索"] C --> D["サポートベクター\nを特定"] D --> E["決定境界\nw·x + b = 0"] E --> F["クラス分類\n+1 / −1"] style A fill:#2563eb,color:#fff style C fill:#1e40af,color:#fff style F fill:#10b981,color:#fff

数式で見る #

線形に分離可能な場合は次の最適化問題を解きます。

$$ \min_{\mathbf{w}, b} \ \frac{1}{2} \lVert \mathbf{w} \rVert_2^2 \quad \text{s.t.} \quad y_i(\mathbf{w}^\top \mathbf{x}_i + b) \ge 1. $$

実際のデータでは完全に分離できないことが多いため、スラック変数 \(\xi_i \ge 0\) を導入したソフトマージン SVM を用います。

$$ \min_{\mathbf{w}, b, \boldsymbol{\xi}} \ \frac{1}{2} \lVert \mathbf{w} \rVert_2^2 + C \sum_{i=1}^{n} \xi_i \quad \text{s.t.} \quad y_i(\mathbf{w}^\top \mathbf{x}_i + b) \ge 1 - \xi_i. $$

内積 \(\mathbf{x}_i^\top \mathbf{x}_j\) をカーネル \(K(\mathbf{x}_i, \mathbf{x}_j)\) に置き換えれば、非線形な決定境界も表現できます。

アルゴリズムの詳細 #

双対問題 #

ソフトマージンSVMの主問題にラグランジュ乗数\(\alpha_i \ge 0\)を導入すると、以下の双対問題が得られます。

$$ \max_{\boldsymbol{\alpha}} \sum_{i=1}^{n} \alpha_i - \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j K(\mathbf{x}_i, \mathbf{x}_j) $$$$ \text{s.t.} \quad 0 \le \alpha_i \le C, \quad \sum_{i=1}^{n} \alpha_i y_i = 0 $$

この双対問題は凸二次計画問題であり、大域的最適解が保証されます。内積\(\mathbf{x}_i^\top \mathbf{x}_j\)をカーネル関数\(K(\mathbf{x}_i, \mathbf{x}_j)\)に置き換えることで、入力空間での明示的な写像なしに高次元空間での分離が可能になります。

KKT条件とサポートベクター #

最適解はKKT（Karush-Kuhn-Tucker）条件を満たします。

$$ \alpha_i \bigl[ y_i(\mathbf{w}^\top \mathbf{x}_i + b) - 1 + \xi_i \bigr] = 0 $$$$ (C - \alpha_i)\,\xi_i = 0 $$

これにより、各サンプルは\(\alpha_i\)の値に応じて3つのカテゴリーに分類されます。

\(\alpha_i\) の値サンプルの役割位置
\(\alpha_i = 0\)非サポートベクターマージン外側（正しく分類）
\(0 < \alpha_i < C\)マージン上のサポートベクター\(y_i(\mathbf{w}^\top \mathbf{x}_i + b) = 1\)
\(\alpha_i = C\)マージン内側のサポートベクター誤分類またはマージン違反

バイアス項\(b\)は、\(0 < \alpha_i < C\)を満たすサポートベクターから計算されます。

決定関数 #

学習後の予測は、サポートベクターのみを使って以下で計算されます。

$$ f(\mathbf{x}) = \operatorname{sign}\left(\sum_{i \in \text{SV}} \alpha_i\, y_i\, K(\mathbf{x}_i, \mathbf{x}) + b\right) $$

サポートベクター以外のサンプル（\(\alpha_i = 0\)）は決定関数に寄与しないため、訓練データの大部分を捨てても予測が変わりません。これがSVMのスパース性です。

カーネル関数 #

カーネル関数は\(K(\mathbf{x}_i, \mathbf{x}_j) = \langle \phi(\mathbf{x}_i), \phi(\mathbf{x}_j) \rangle\)を満たす関数で、高次元空間への写像\(\phi\)を明示的に計算せずに内積を求められます。Mercerの定理により、正定値カーネルであれば対応する特徴空間が存在することが保証されます。

カーネル数式特徴
線形\(K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^\top \mathbf{x}_j\)計算が高速、線形分離可能なデータ向け
多項式\(K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma, \mathbf{x}_i^\top \mathbf{x}_j + r)^d\)交互作用を考慮、\(d\)で非線形度を制御
RBF\(K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma \lVert \mathbf{x}_i - \mathbf{x}_j \rVert^2)\)無限次元空間への写像、汎用的
シグモイド\(K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\gamma, \mathbf{x}_i^\top \mathbf{x}_j + r)\)ニューラルネットワークとの類似性

SMOアルゴリズム #

双対問題の求解には**SMO（Sequential Minimal Optimization）**が広く使われます。SMOは2つの\(\alpha_i\)を同時に選んで解析的に更新するため、大規模な二次計画ソルバーを必要としません。

  1. KKT条件に違反する\(\alpha_i\)を選択します
  2. 対応するもう1つの\(\alpha_j\)をヒューリスティックで選びます
  3. \(\alpha_i, \alpha_j\)を制約\(\sum \alpha_k y_k = 0\)のもとで解析的に更新します
  4. すべての\(\alpha\)がKKT条件を満たすまで繰り返します
flowchart TD A["主問題\n(ソフトマージン)"] --> B["ラグランジュ双対\nα_i を導入"] B --> C["双対問題\n凸二次計画"] C --> D["SMOで求解\n2変数ずつ更新"] D --> E["KKT条件の確認"] E --> F{"全サンプル\n満足？"} F -->|No| D F -->|Yes| G["サポートベクター特定\nα_i > 0"] G --> H["決定関数\nf(x) = Σα_i y_i K(x_i,x) + b"] style A fill:#2563eb,color:#fff style D fill:#1e40af,color:#fff style H fill:#10b981,color:#fff

参考リンク

Boser, B. E., Guyon, I. M., & Vapnik, V. N. (1992). A Training Algorithm for Optimal Margin Classifiers. Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory (COLT), 144–152.

Platt, J. C. (1998). Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines. Microsoft Research Technical Report MSR-TR-98-14.

SVMは特徴量のスケールに非常に敏感です。正規化なしで学習すると、大きいスケールの特徴量がマージンを支配し、性能が大きく低下します。必ず StandardScaler を適用してください。

Pythonによる実験 #

次のコードは make_moons で生成した非線形データに線形カーネル SVM と RBF カーネル SVM を適用し、決定境界を比較する例です。RBF カーネルの方が曲がった境界を適切に表現できることがわかります。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons
from sklearn.metrics import accuracy_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

def run_svm_demo(
    n_samples: int = 400,
    noise: float = 0.25,
    random_state: int = 42,
    title: str = "RBF カーネル SVM の決定境界",
    xlabel: str = "特徴量1",
    ylabel: str = "特徴量2",
) -> dict[str, float]:
    """Train linear and RBF SVMs and plot the RBF decision boundary."""
    X, y = make_moons(n_samples=n_samples, noise=noise, random_state=random_state)

    linear_clf = make_pipeline(StandardScaler(), SVC(kernel="linear", C=1.0))
    linear_clf.fit(X, y)

    rbf_clf = make_pipeline(StandardScaler(), SVC(kernel="rbf", C=5.0, gamma=0.5))
    rbf_clf.fit(X, y)

    linear_acc = float(accuracy_score(y, linear_clf.predict(X)))
    rbf_acc = float(accuracy_score(y, rbf_clf.predict(X)))

    grid_x, grid_y = np.meshgrid(
        np.linspace(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, 400),
        np.linspace(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, 400),
    )
    grid = np.c_[grid_x.ravel(), grid_y.ravel()]
    rbf_scores = rbf_clf.predict(grid).reshape(grid_x.shape)

    fig, ax = plt.subplots(figsize=(6, 5))
    ax.contourf(grid_x, grid_y, rbf_scores, alpha=0.2, cmap="coolwarm")
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k", s=30)
    ax.set_title(title)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    fig.tight_layout()
    plt.show()

    return {"linear_accuracy": linear_acc, "rbf_accuracy": rbf_acc}

metrics = run_svm_demo(
    title="RBF カーネル SVM の決定境界",
    xlabel="特徴量1",
    ylabel="特徴量2",
)
print(f"線形カーネルの精度: {metrics['linear_accuracy']:.3f}")
print(f"RBF カーネルの精度: {metrics['rbf_accuracy']:.3f}")

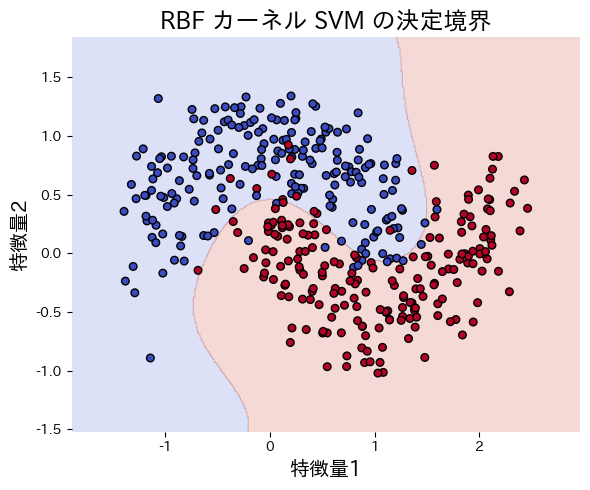
RBF カーネルの方が曲がった境界を適切に表現できることがわかりますの図

カーネル選択に迷った場合は、まずRBF（kernel="rbf"）から試してください。RBFは非線形な境界を汎用的に表現でき、多くのケースでベースラインとして機能します。C と gamma は GridSearchCV で探索するのが効率的です。

罰則 C と決定境界 #

C を変えるとサポートベクタマシンのマージンと境界がどう変化するか確認できます。

まとめ #

  • SVMはクラス間のマージンを最大化する超平面を学習することで、汎化性能の高い分類器を構築します。
  • ソフトマージンのペナルティ係数 \(C\) でマージン幅と誤分類のトレードオフを制御できます。
  • カーネルトリックにより、特徴量を明示的に増やさずに非線形な決定境界を扱えます。
  • 標準化と \(C\)・\(\gamma\) のハイパーパラメーター探索が安定した性能発揮の鍵となります。

参考文献 #

  • Vapnik, V. (1998). Statistical Learning Theory. Wiley.
  • Smola, A. J., & Schölkopf, B. (2004). A Tutorial on Support Vector Regression. Statistics and Computing, 14(3), 199 E22.