まとめ- k-means++はセントロイド同士が離れるように初期化し、k-meansが局所解に陥るリスクを下げる。
- 新しいセントロイドは既存のセントロイドからの距離二乗に比例する確率で選ばれるため、代表点が偏りにくい。
- scikit-learnでは
KMeans(init="k-means++")がデフォルトで有効になっている。
直感
#
k-meansの結果は初期セントロイドの位置に大きく左右される。たまたま近い位置に2つのセントロイドが配置されると、片方のクラスターが空になったり、最適な分割から遠い解に収束したりする。k-means++は「すでに選ばれたセントロイドから遠い点ほど次のセントロイドに選ばれやすい」という確率的な初期化を行い、初期配置の偏りを防ぐ。
flowchart LR
A["1点目を\nランダム選択"] --> B["各点の距離\nD(x)を計算"]
B --> C["D(x)²に比例する\n確率で次を選択"]
C --> D{"k個\n揃った?"}
D -->|No| B
D -->|Yes| E["k-meansを\n実行"]
E --> F["安定した\nクラスター"]
style A fill:#2563eb,color:#fff
style C fill:#1e40af,color:#fff
style F fill:#10b981,color:#fff
詳細な解説
#
Arthur, David, and Sergei Vassilvitskii. “k-means++: The advantages of careful seeding.” SODA 2007.
ライブラリと実験データ
#
1
2
3
4
| import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
|
クラスター間の距離が近い、やや難しいデータを生成します。
1
2
3
4
5
6
| X, y_true = make_blobs(
n_samples=500,
centers=[[-3, 0], [0, 0], [3, 0]],
cluster_std=1.2,
random_state=42,
)
|
ランダム初期化 vs k-means++
#
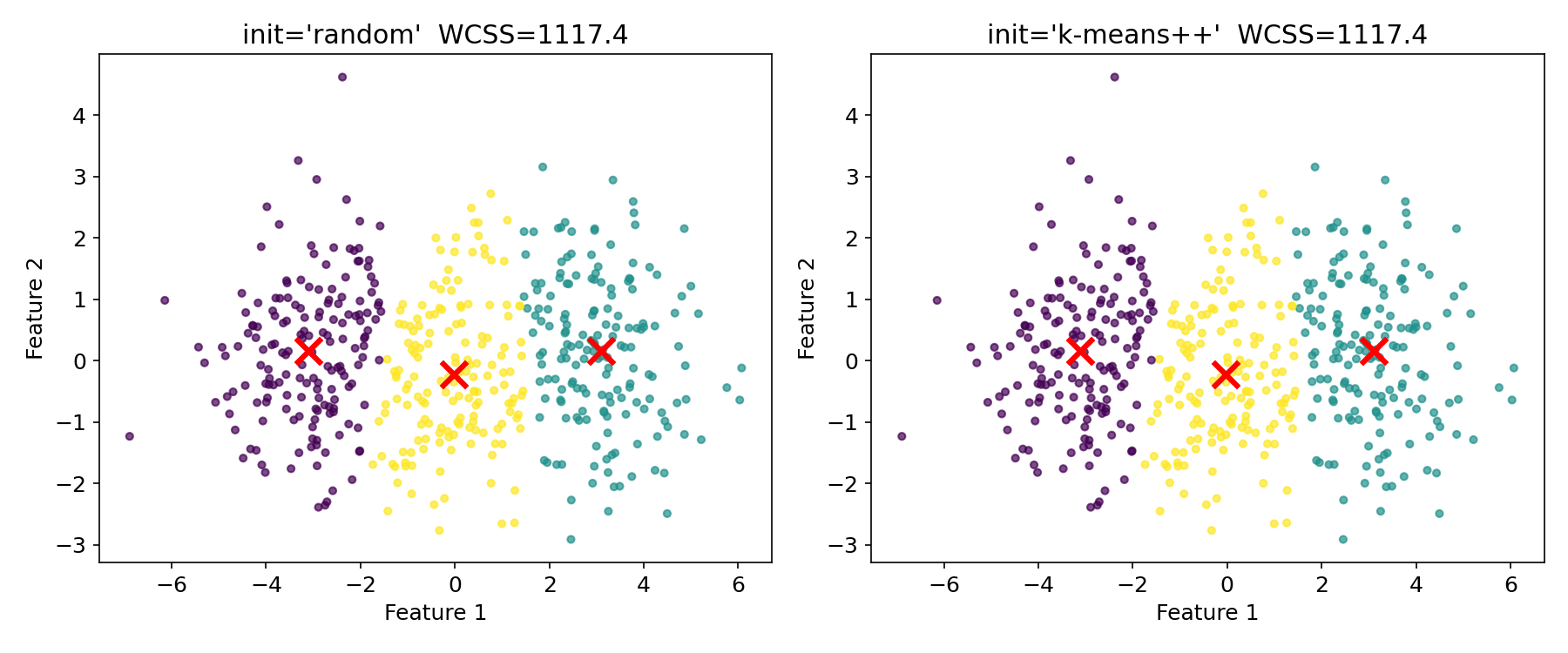
同じデータに対して、ランダム初期化とk-means++の結果を比較します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| fig, axes = plt.subplots(1, 2, figsize=(12, 5))
for ax, init_method in zip(axes, ["random", "k-means++"]):
km = KMeans(n_clusters=3, init=init_method, n_init=1, random_state=0)
labels = km.fit_predict(X)
ax.scatter(X[:, 0], X[:, 1], c=labels, cmap="viridis", s=15, alpha=0.7)
ax.scatter(
km.cluster_centers_[:, 0], km.cluster_centers_[:, 1],
c="red", marker="x", s=200, linewidths=3,
)
ax.set_title(f"init='{init_method}' WCSS={km.inertia_:.1f}")
plt.tight_layout()
plt.show()
|
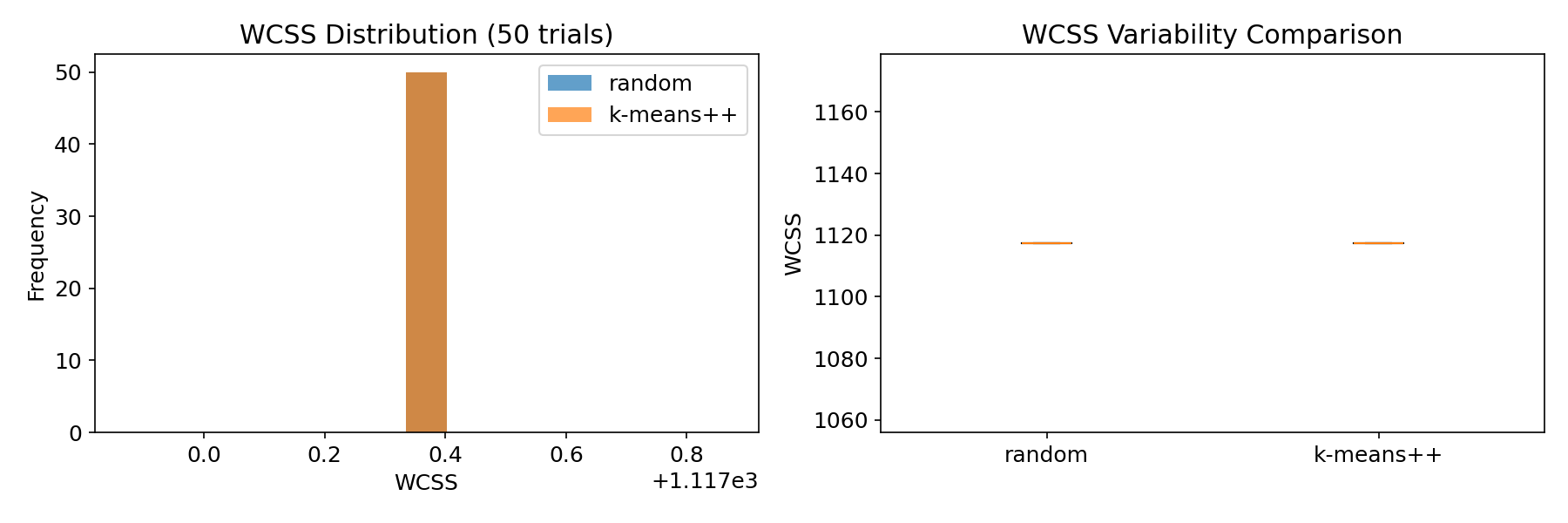
複数試行での安定性の比較
#
n_init=1の試行を50回繰り返し、WCSSのばらつきを比較します。k-means++のほうがばらつきが小さく、安定した結果を返します。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| random_scores = []
pp_scores = []
for seed in range(50):
km_r = KMeans(n_clusters=3, init="random", n_init=1, random_state=seed)
km_r.fit(X)
random_scores.append(km_r.inertia_)
km_pp = KMeans(n_clusters=3, init="k-means++", n_init=1, random_state=seed)
km_pp.fit(X)
pp_scores.append(km_pp.inertia_)
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
axes[0].hist(random_scores, bins=15, alpha=0.7, label="random")
axes[0].hist(pp_scores, bins=15, alpha=0.7, label="k-means++")
axes[0].set_xlabel("WCSS")
axes[0].set_ylabel("頻度")
axes[0].set_title("WCSSの分布(50回試行)")
axes[0].legend()
axes[1].boxplot(
[random_scores, pp_scores],
labels=["random", "k-means++"],
)
axes[1].set_ylabel("WCSS")
axes[1].set_title("WCSSのばらつき比較")
plt.tight_layout()
plt.show()
print(f"random 平均WCSS: {np.mean(random_scores):.1f} 標準偏差: {np.std(random_scores):.1f}")
print(f"k-means++ 平均WCSS: {np.mean(pp_scores):.1f} 標準偏差: {np.std(pp_scores):.1f}")
|
k-means++の初期化アルゴリズム
#
k-means++の初期化は以下の手順で行われます。
- データからランダムに1つ目のセントロイドを選ぶ
- 各データ点について、もっとも近いセントロイドまでの距離 \(D(x)\) を計算する
- \(D(x)^2\) に比例する確率で次のセントロイドを選ぶ
- 手順2〜3を \(k\) 個のセントロイドが揃うまで繰り返す
距離が遠い点ほど選ばれやすいため、セントロイドがデータ全体にバランスよく配置されます。
Mini-Batch k-means
#
大規模データではミニバッチを使った近似版が実用的です。各イテレーションでデータの一部だけを使ってセントロイドを更新するため、計算量が大幅に減ります。
1
2
3
4
5
6
7
| from sklearn.cluster import MiniBatchKMeans
mbkm = MiniBatchKMeans(n_clusters=3, batch_size=100, random_state=42)
labels_mb = mbkm.fit_predict(X)
print(f"Mini-Batch k-means WCSS: {mbkm.inertia_:.1f}")
print(f"通常 k-means WCSS: {KMeans(n_clusters=3, random_state=42).fit(X).inertia_:.1f}")
|
k-means++は初期化を改善しますが、k-meansの根本的な制約(球状クラスター仮定、\(k\) の事前指定)は解消しません。クラスターの形状が非凸な場合や、クラスター数が不明な場合はDBSCANやHDBSCANも検討してください。
scikit-learnのKMeansはinit="k-means++"がデフォルトなので、特に指定しなくても恩恵を受けられます。さらに安定性を高めたい場合はn_init=10以上を設定してください。大規模データではMiniBatchKMeansで計算コストを抑えられます。
まとめ
#
- k-means++は距離二乗に比例する確率でセントロイドを選ぶことで、初期配置の偏りを防ぎます。
- ランダム初期化と比較して、WCSSのばらつきが小さく安定した結果を返します。
- scikit-learnではデフォルトで有効になっているため、とくに設定しなくても利用できます。
- 大規模データではMiniBatchKMeansと組み合わせることで、精度を保ちながら計算コストを削減できます。

