まとめ- X-meansはK-meansを拡張し、BIC/MDL基準でクラスタ分割の妥当性を評価しながらクラスタ数を自動推定する。
- 初期クラスタ数と上限クラスタ数の設定で探索範囲を制御し、過分割を抑えながら柔軟に分割できる。
- K-means固定kとの比較により、クラスタ数推定が分析結果に与える影響を検証できる。
- k-means — X-means は k-means を拡張してクラスター数を自動推定します
直感
#
X-meansは『まず粗く分けて、分ける価値があるクラスタだけ追加分割する』戦略です。すべてを一度に最適化するのではなく、統計基準で局所的に分割可否を判断するため、kの手動探索を減らせます。
詳細な解説
#
<p><b>X-means</b>とはクラスタリングのアルゴリズムの一種で、クラスタリングを進める中でクラスタ数を自動的に決定します。k-means++でkを指定してクラスタリングを実行した場合と、X-meansの結果を比較します。</p>
Pelleg, Dan, and Andrew W. Moore. “X-means: Extending k-means with efficient estimation of the number of clusters.” Icml. Vol. 1. 2000.
1
2
3
4
5
| import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
|
k-meansでkをあらかじめ指定
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| def plot_by_kmeans(X, k=5):
y_pred = KMeans(n_clusters=k, random_state=random_state, init="random").fit_predict(
X
)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, marker="x")
plt.title(f"k-means, n_clusters={k}")
# サンプルデータを作成
n_samples = 1000
random_state = 117117
X, _ = make_blobs(
n_samples=n_samples, random_state=random_state, cluster_std=1, centers=10
)
# k-means++を実行
plot_by_kmeans(X)
|

x-meanでクラスタ数を指定せずに実行
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
| from pyclustering.cluster.xmeans import xmeans
from pyclustering.cluster.center_initializer import kmeans_plusplus_initializer
BAYESIAN_INFORMATION_CRITERION = 0
MINIMUM_NOISELESS_DESCRIPTION_LENGTH = 1
def plot_by_xmeans(
X, c_min=3, c_max=10, criterion=BAYESIAN_INFORMATION_CRITERION, tolerance=0.025
):
initial_centers = kmeans_plusplus_initializer(X, c_min).initialize()
xmeans_instance = xmeans(
X, initial_centers, c_max, criterion=criterion, tolerance=tolerance
)
xmeans_instance.process()
# プロット用のデータを作成
clusters = xmeans_instance.get_clusters()
n_samples = X.shape[0]
c = []
for i, cluster_i in enumerate(clusters):
X_ci = X[cluster_i]
color_ci = [i for _ in cluster_i]
plt.scatter(X_ci[:, 0], X_ci[:, 1], marker="x")
plt.title("x-means")
# x-meansを実行
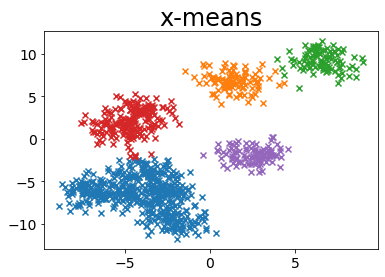
plot_by_xmeans(X, c_min=3, c_max=10, criterion=BAYESIAN_INFORMATION_CRITERION)
|
MINIMUM_NOISELESS_DESCRIPTION_LENGTH
#
1
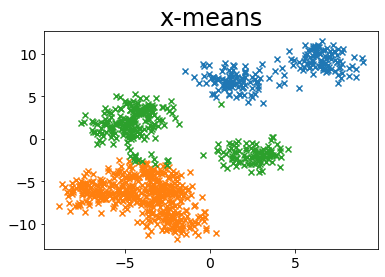
| plot_by_xmeans(X, c_min=3, c_max=10, criterion=MINIMUM_NOISELESS_DESCRIPTION_LENGTH)
|
toleranceの影響
#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| X, _ = make_blobs(
n_samples=2000,
random_state=random_state,
cluster_std=0.4,
centers=10,
)
plt.figure(figsize=(25, 5))
for i, ti in enumerate(np.linspace(0.0001, 1, 5)):
ti = np.round(ti, 4)
plt.subplot(1, 10, i + 1)
plot_by_xmeans(
X, c_min=3, c_max=10, criterion=BAYESIAN_INFORMATION_CRITERION, tolerance=ti
)
plt.title(f"tol={ti}")
|

色々なデータに対して k-means と x-means を比較する
#
1
2
3
4
5
6
7
8
9
10
11
12
13
| for i in range(5):
X, _ = make_blobs(
n_samples=n_samples,
random_state=random_state,
cluster_std=0.7,
centers=5 + i * 5,
)
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plot_by_kmeans(X)
plt.subplot(1, 2, 2)
plot_by_xmeans(X, c_min=3, c_max=20)
plt.show()
|
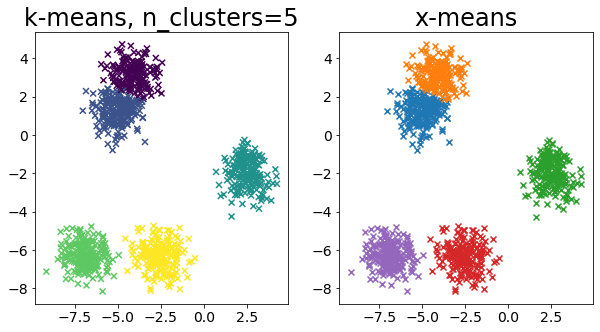

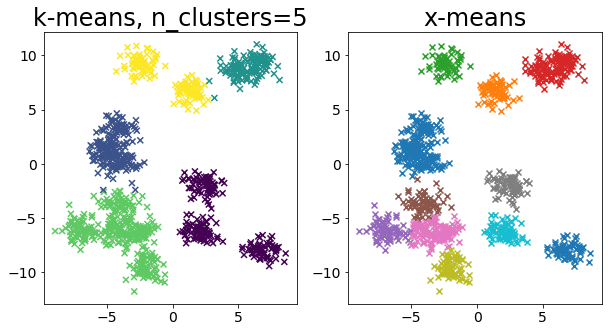
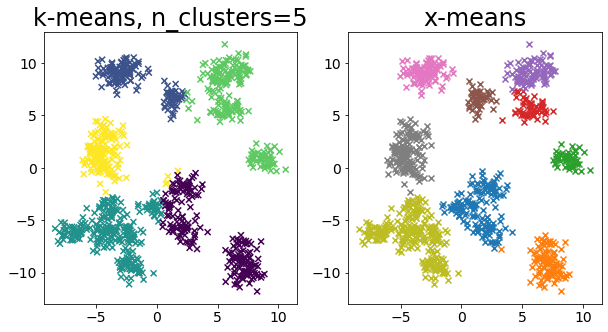
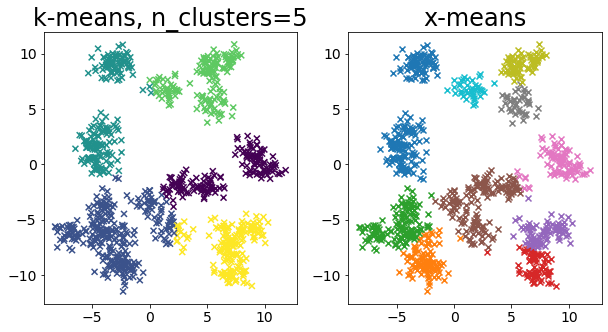
クラスタ数と K-Means
#
クラスタ数 k を変えるとシルエット係数がどう変化するか確認できます。








