ベイズ線形回帰 | 予測の不確実性まで推論する

まとめ

ベイズ線形回帰は係数を確率変数として扱い、予測値と不確実性を同時に推定できる。
事前分布と尤度から事後分布を解析的に求められ、小規模データや外れ値に対して頑健に振る舞う。
予測分布がガウス形となるため、平均と分散を可視化して意思決定に活用できる。
BayesianRidge を使えばノイズ分散まで自動調整され、実務導入が容易になる。

直感 #

最小二乗法は「最もありそうな係数」を 1 組だけ推定しますが、現実のデータではその推定にも不確実性が残ります。ベイズ線形回帰では係数を確率分布として推論し、観測データと事前知識を組み合わせることで予測値の平均と幅の両方を得られます。データが少ない場面でも、モデルがどの程度自信を持っているのかを可視化できるのが強みです。

具体的な数式 #

係数ベクトル $\boldsymbol\beta$ に平均 0、分散 $\tau^{-1}$ の多変量ガウス事前分布を置き、観測ノイズ $\epsilon_i \sim \mathcal{N}(0, \alpha^{-1})$ を仮定すると、事後分布は

$$ p(\boldsymbol\beta \mid \mathbf{X}, \mathbf{y}) = \mathcal{N}(\boldsymbol\beta \mid \boldsymbol\mu, \mathbf{\Sigma}) $$

となります。ここで

$$ \mathbf{\Sigma} = (\alpha \mathbf{X}^\top \mathbf{X} + \tau \mathbf{I})^{-1}, \qquad \boldsymbol\mu = \alpha \mathbf{\Sigma} \mathbf{X}^\top \mathbf{y} $$

です。予測分布もガウス形となり、入力 $\mathbf{x}*$ に対して $\mathcal{N}(\hat{y}, \sigma_^2)$ が得られます。scikit-learn の BayesianRidge は $\alpha$ と $\tau$ もデータから推定してくれるため、手軽にこの枠組みを利用できます。

Pythonを用いた実験や説明 #

外れ値を含む一次関数データで、最尤推定による線形回帰とベイズ線形回帰を比較します。

from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import BayesianRidge, LinearRegression
from sklearn.metrics import mean_squared_error


def run_bayesian_linear_demo(
    n_samples: int = 120,
    noise_scale: float = 1.0,
    outlier_count: int = 6,
    outlier_scale: float = 8.0,
    label_observations: str = "observations",
    label_ols: str = "OLS",
    label_bayes: str = "Bayesian mean",
    label_interval: str = "95% CI",
    xlabel: str = "input $",
    ylabel: str = "output $",
    title: str | None = None,
) -> dict[str, float]:
    """Fit OLS and Bayesian ridge to noisy data with outliers, plotting results.

    Args:
        n_samples: Number of evenly spaced sample points.
        noise_scale: Standard deviation of Gaussian noise added to the base line.
        outlier_count: Number of indices to perturb strongly.
        outlier_scale: Standard deviation for the outlier noise.
        label_observations: Legend label for observations.
        label_ols: Label for the ordinary least squares line.
        label_bayes: Label for the Bayesian posterior mean line.
        label_interval: Label for the confidence interval band.
        xlabel: X-axis label.
        ylabel: Y-axis label.
        title: Optional plot title.

    Returns:
        Dictionary containing MSEs and coefficients statistics.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(seed=0)

    x_values: np.ndarray = np.linspace(-4.0, 4.0, n_samples, dtype=float)
    y_clean: np.ndarray = 1.8 * x_values - 0.5
    y_noisy: np.ndarray = y_clean + rng.normal(scale=noise_scale, size=x_values.shape)

    outlier_idx = rng.choice(n_samples, size=outlier_count, replace=False)
    y_noisy[outlier_idx] += rng.normal(scale=outlier_scale, size=outlier_idx.shape)

    X: np.ndarray = x_values[:, np.newaxis]

    ols = LinearRegression()
    ols.fit(X, y_noisy)
    bayes = BayesianRidge(compute_score=True)
    bayes.fit(X, y_noisy)

    X_grid: np.ndarray = np.linspace(-6.0, 6.0, 200, dtype=float)[:, np.newaxis]
    ols_mean: np.ndarray = ols.predict(X_grid)
    bayes_mean, bayes_std = bayes.predict(X_grid, return_std=True)

    metrics = {
        "ols_mse": float(mean_squared_error(y_noisy, ols.predict(X))),
        "bayes_mse": float(mean_squared_error(y_noisy, bayes.predict(X))),
        "coef_mean": float(bayes.coef_[0]),
        "coef_std": float(np.sqrt(bayes.sigma_[0, 0])),
    }

    upper = bayes_mean + 1.96 * bayes_std
    lower = bayes_mean - 1.96 * bayes_std

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y_noisy, color="#ff7f0e", alpha=0.6, label=label_observations)
    ax.plot(X_grid, ols_mean, color="#1f77b4", linestyle="--", label=label_ols)
    ax.plot(X_grid, bayes_mean, color="#2ca02c", linewidth=2, label=label_bayes)
    ax.fill_between(
        X_grid.ravel(),
        lower,
        upper,
        color="#2ca02c",
        alpha=0.2,
        label=label_interval,
    )
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return metrics



metrics = run_bayesian_linear_demo(
    label_observations="観測データ",
    label_ols="最小二乗法",
    label_bayes="ベイズ平均",
    label_interval="95% 信頼区間",
    xlabel="入力 $",
    ylabel="出力 $",
    title="ベイズ回帰とOLSの比較",
)
print(f"OLSのMSE: {metrics['ols_mse']:.3f}")
print(f"ベイズ回帰のMSE: {metrics['bayes_mse']:.3f}")
print(f"係数の事後平均: {metrics['coef_mean']:.3f}")
print(f"係数の事後標準偏差: {metrics['coef_std']:.3f}")

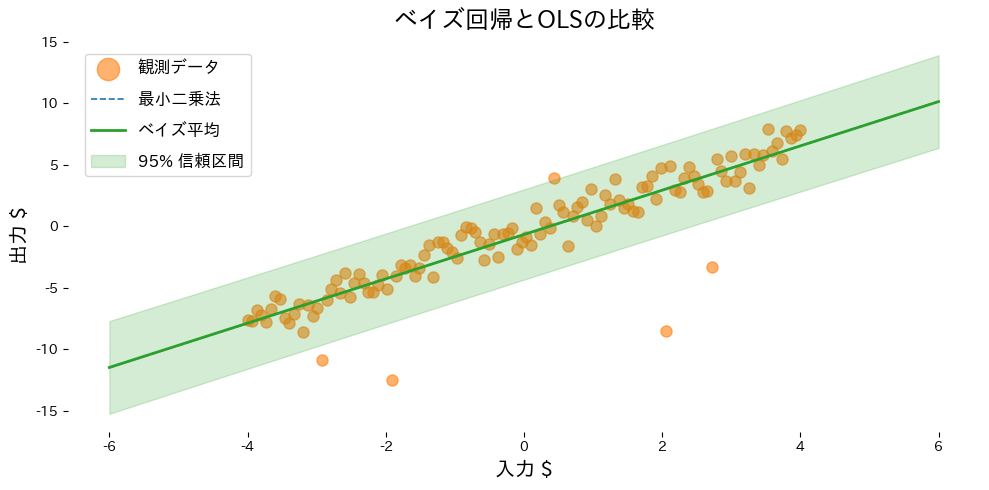
外れ値を含む一次関数データで、最尤推定による線形回帰とベイズ線形回帰を比較しますの図

実行結果の読み方 #

OLS は外れ値に引きずられて直線が傾きやすいが、ベイズ線形回帰は平均の変動が抑えられる。
return_std=True で得られた標準偏差から、予測の信頼区間を簡単に描ける。
係数の事後分散を確認すると、どの特徴量に不確実性が残っているかを把握できる。

参考文献 #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.