2.1.8
主成分回帰 (PCR)
まとめ
- 主成分回帰 (PCR) は PCA で特徴量を圧縮してから線形回帰を行い、多重共線性による不安定さを抑える。
- 主成分はデータの分散が大きい方向を優先するため、ノイズの多い軸を削り情報を保ったままモデルを構築できる。
- 残す主成分数を調整することで、過学習を防ぎながら計算量も削減できる。
- 標準化や欠損値処理などの前処理を整えることが精度向上と解釈の土台になる。
直感 #
説明変数同士に強い相関があると、最小二乗法では係数が過度に変動したり解釈が難しくなります。PCR はまず PCA で相関のある軸をまとめ、情報量の多い順に並べ替えた主成分スコアだけを用いて回帰します。重要な変動だけを残すことで、安定した回帰係数を得ようという発想です。
具体的な数式 #
標準化した説明変数行列 \(\mathbf{X}\) に PCA を適用し、固有値の大きいものから \(k\) 個の主成分を選びます。主成分スコアを \(\mathbf{Z} = \mathbf{X} \mathbf{W}_k\) とすると、回帰モデルは
$$ y = \boldsymbol{\gamma}^\top \mathbf{Z} + b $$で学習されます。最終的に元の特徴量空間の係数は \(\boldsymbol{\beta} = \mathbf{W}_k \boldsymbol{\gamma}\) として復元できます。主成分数 \(k\) は累積寄与率や交差検証で選ぶのが一般的です。
Pythonを用いた実験や説明 #
糖尿病データセットを使って主成分数ごとの交差検証スコアを比較します。
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
def evaluate_pcr_components(
cv_folds: int = 5,
xlabel: str = "Number of components k",
ylabel: str = "CV MSE (lower is better)",
title: str | None = None,
label_best: str = "best={k}",
) -> dict[str, float]:
"""Cross-validate PCR with varying component counts and plot the curve.
Args:
cv_folds: Number of folds for cross-validation.
xlabel: Label for the component-count axis.
ylabel: Label for the error axis.
title: Optional title for the plot.
label_best: Format string for highlighting the best component count.
Returns:
Dictionary containing the best component count and its CV score.
"""
X, y = load_diabetes(return_X_y=True)
def build_pcr(n_components: int) -> Pipeline:
return Pipeline([
("scale", StandardScaler()),
("pca", PCA(n_components=n_components, random_state=0)),
("reg", LinearRegression()),
])
components = np.arange(1, X.shape[1] + 1)
cv_scores = []
for k in components:
model = build_pcr(int(k))
score = cross_val_score(
model,
X,
y,
cv=cv_folds,
scoring="neg_mean_squared_error",
)
cv_scores.append(score.mean())
cv_scores_arr = np.array(cv_scores)
best_idx = int(np.argmax(cv_scores_arr))
best_k = int(components[best_idx])
best_mse = float(-cv_scores_arr[best_idx])
best_model = build_pcr(best_k).fit(X, y)
explained = best_model["pca"].explained_variance_ratio_
fig, ax = plt.subplots(figsize=(8, 4))
ax.plot(components, -cv_scores_arr, marker="o")
ax.axvline(best_k, color="red", linestyle="--", label=label_best.format(k=best_k))
ax.set_xlabel(xlabel)
ax.set_ylabel(ylabel)
if title:
ax.set_title(title)
ax.legend()
fig.tight_layout()
plt.show()
return {
"best_k": best_k,
"best_mse": best_mse,
"explained_variance_ratio": explained,
}
metrics = evaluate_pcr_components(
xlabel="主成分の数 k",
ylabel="CV MSE (小さいほど良い)",
title="PCR の主成分数と汎化誤差",
label_best="最適k={k}",
)
print(f"最適な主成分数: {metrics['best_k']}")
print(f"最適CV MSE: {metrics['best_mse']:.3f}")
print("寄与率:", metrics['explained_variance_ratio'])
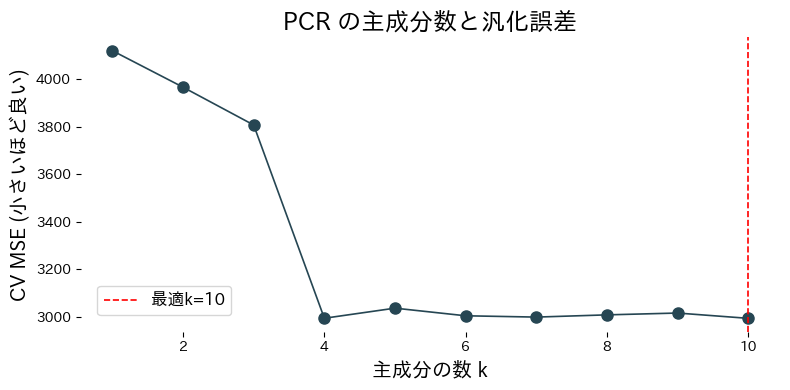
実行結果の読み方 #
- 主成分数を増やすと訓練データへの適合が上がるが、交差検証 MSE が最小となるポイントがある。
- PCA の寄与率を確認すると、どの主成分が全体の説明力に貢献しているかを把握できる。
- 主成分の負荷量を調べれば、どの特徴量が各主成分に強く寄与しているかが分かる。
参考文献 #
- Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.
- Massy, W. F. (1965). Principal Components Regression in Exploratory Statistical Research. Journal of the American Statistical Association, 60(309), 234–256.