リッジ・ラッソ

中級

2.1.2

リッジ・ラッソ

最終更新 2020-02-12 読了時間 3 分
まとめ
  • リッジ回帰は L2 正則化によって係数を滑らかに縮小し、多重共線性があっても安定した推定を行う。
  • ラッソ回帰は L1 正則化により一部の係数を 0 にし、特徴量選択とモデルの解釈性向上に寄与する。
  • 正則化強度 \(\alpha\) を調整することで、学習データへの適合と汎化性能のバランスを取れる。
  • 標準化と交差検証を組み合わせると、過学習を抑えながら最適なハイパーパラメータを選択しやすい。
  • 線形回帰 の概念を先に学ぶと理解がスムーズです

直感 #

最小二乗法は外れ値や説明変数間の強い相関に弱く、係数が極端な値になってしまうことがあります。リッジ回帰とラッソ回帰は、係数が大きくなりすぎないようペナルティを加えることで、予測性能と解釈性のバランスをとるための拡張です。リッジは「全体を滑らかに縮める」イメージ、ラッソは「不要な係数を大胆に 0 にする」イメージで捉えると理解しやすくなります。

flowchart LR A["入力データX, y"] --> B["SSE\n残差二乗和"] B --> C{"正則化の種類"} C -->|L2| D["リッジ\n係数を縮小"] C -->|L1| E["ラッソ\n係数を0に"] D --> F["安定した\n係数推定"] E --> F style A fill:#2563eb,color:#fff style C fill:#1e40af,color:#fff style F fill:#10b981,color:#fff

具体的な数式 #

リッジ回帰とラッソ回帰の目的関数は、最小二乗誤差にそれぞれ L2・L1 ノルムのペナルティを加えた形になります。

  • リッジ回帰

    $$ \min_{\boldsymbol\beta, b} \sum_{i=1}^{n} \left(y_i - (\boldsymbol\beta^\top \mathbf{x}_i + b)\right)^2 + \alpha \lVert \boldsymbol\beta \rVert_2^2 $$

  • ラッソ回帰

    $$ \min_{\boldsymbol\beta, b} \sum_{i=1}^{n} \left(y_i - (\boldsymbol\beta^\top \mathbf{x}_i + b)\right)^2 + \alpha \lVert \boldsymbol\beta \rVert_1 $$

\(\alpha\) を大きくすると係数がより強く抑えられます。ラッソでは\(\alpha\) がある閾値を超えると係数が完全に 0 になるため、疎なモデルを得たい場合に有効です。

Pythonを用いた実験や説明 #

以下は重回帰データにリッジ・ラッソ・通常の線形回帰を適用し、係数の大きさと汎化性能を比較する例です。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso, LassoCV, LinearRegression, Ridge, RidgeCV
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

# パラメータ
n_samples = 200
n_features = 10
n_informative = 3
rng = np.random.default_rng(42)

# 真の重み（スパース）
coef = np.zeros(n_features)
coef[:n_informative] = rng.normal(loc=3.0, scale=1.0, size=n_informative)

# 説明変数と目的変数を生成
X = rng.normal(size=(n_samples, n_features))
y = X @ coef + rng.normal(scale=5.0, size=n_samples)

# 各モデルを作成・学習
# with_mean=False にしているのは疎行列対応の書き方の名残かも
linear = make_pipeline(
    StandardScaler(with_mean=False),
    LinearRegression()
).fit(X, y)

ridge = make_pipeline(
    StandardScaler(with_mean=False),
    RidgeCV(alphas=np.logspace(-3, 3, 13), cv=5)
).fit(X, y)

lasso = make_pipeline(
    StandardScaler(with_mean=False),
    LassoCV(alphas=np.logspace(-3, 1, 9), cv=5, max_iter=50_000)
).fit(X, y)

models = {
    "Linear": linear,
    "Ridge": ridge,
    "Lasso": lasso,
}

# 係数の比較可視化
indices = np.arange(n_features)
width = 0.25
plt.figure(figsize=(10, 4))
plt.bar(indices - width, np.abs(linear[-1].coef_), width=width, label="Linear")
plt.bar(indices,         np.abs(ridge[-1].coef_),  width=width, label="Ridge")
plt.bar(indices + width, np.abs(lasso[-1].coef_),  width=width, label="Lasso")
plt.xlabel("特徴量インデックス")
plt.ylabel("|係数|")
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()

# 汎化性能のスコア
for name, model in models.items():
    scores = cross_val_score(model, X, y, cv=5, scoring="r2")
    print(f"{name:>6}: R^2 = {scores.mean():.3f} ± {scores.std():.3f}")

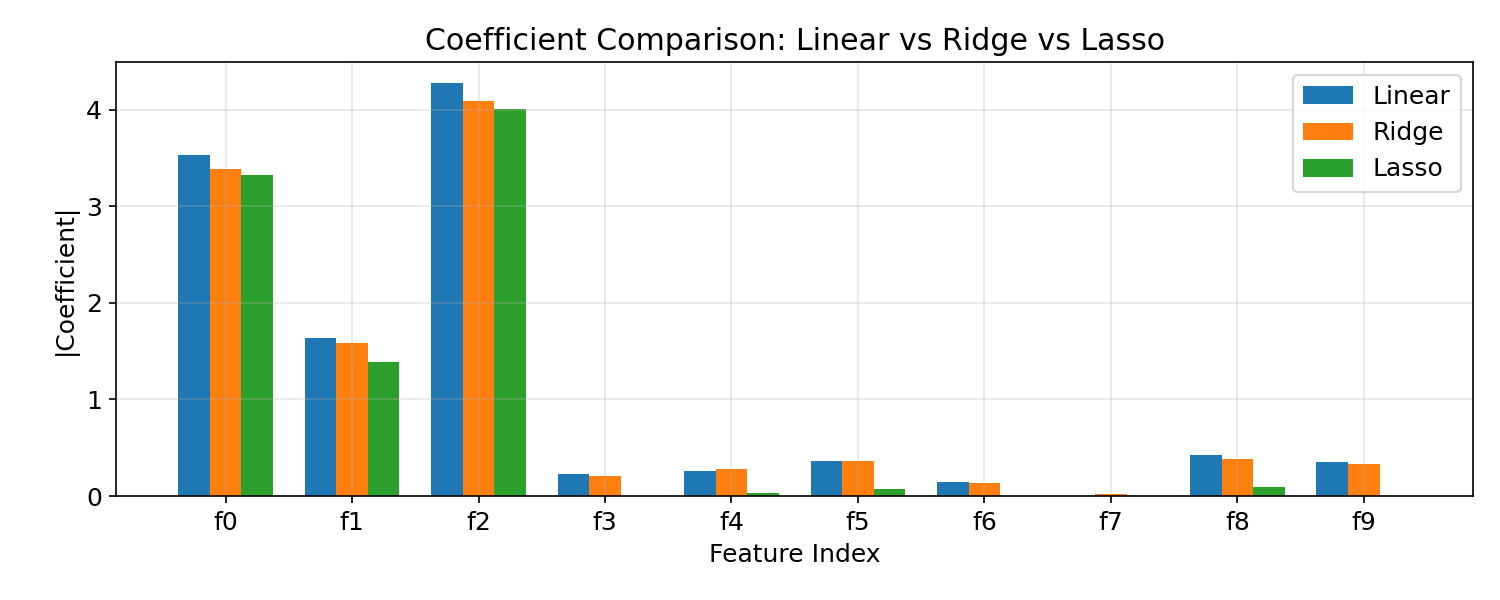
係数の比較：Linear vs Ridge vs Lasso

実行結果の読み方 #

  • リッジはすべての係数を緩やかに縮め、多重共線性があっても安定して推定できます。
  • ラッソは一部の係数を 0 にし、重要な特徴量だけを残す傾向があります。
  • 正則化パラメーターは交差検証で選ぶと、過学習とバイアスのバランスを取りやすくなります。

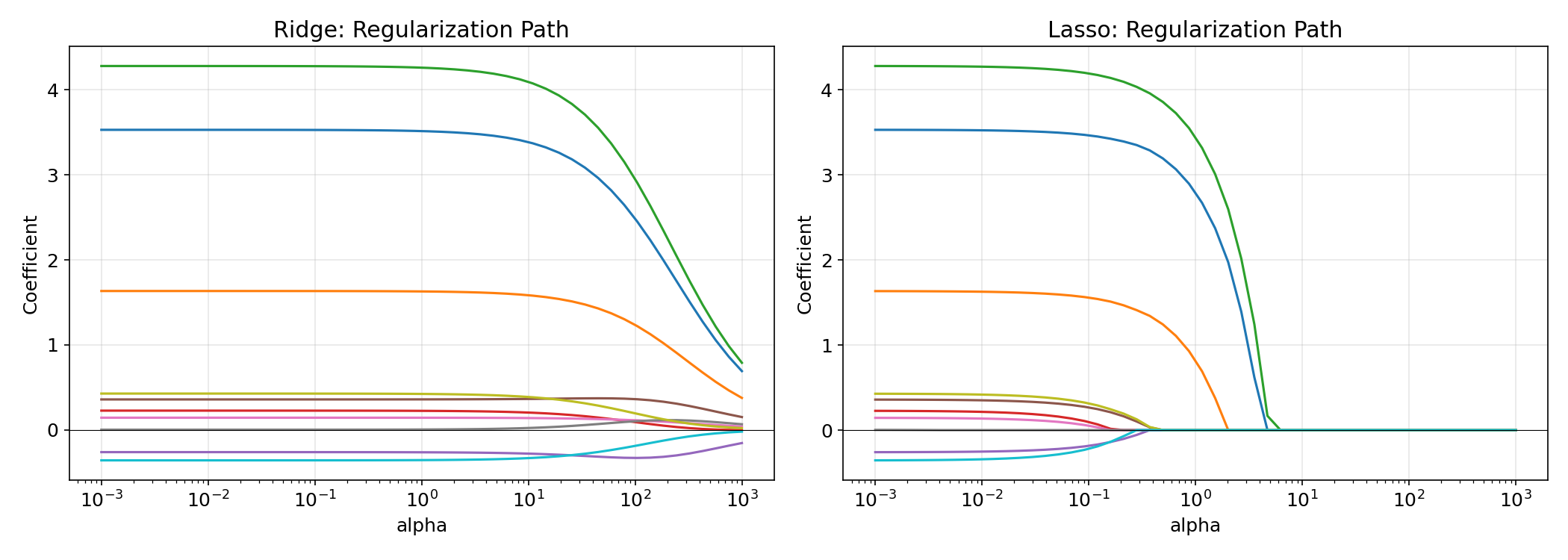
正則化パスの可視化 #

\(\alpha\) を変化させたときの係数の軌跡を正則化パスと呼びます。リッジでは係数が滑らかに 0 に近づき、ラッソではある閾値で急に 0 になる様子が確認できます。

正則化パス：Ridge vs Lasso

リッジ回帰とラッソ回帰は特徴量のスケールに敏感です。標準化（StandardScaler）を適用せずに学習すると、スケールの大きい特徴量が過剰にペナルティを受け、正しい係数推定ができません。必ずパイプラインに標準化を含めてください。

リッジとラッソの使い分けに迷ったら、RidgeCVとLassoCVの両方を試して交差検証スコアを比較してください。特徴量が多く不要な変数が含まれている場合はラッソ、多重共線性が疑われる場合はリッジが有効です。両方の性質が欲しい場合はElastic Netを検討してください。

正則化係数と回帰曲線 #

正則化係数 α を変えると回帰曲線がどう変化するか確認できます。

Ridge の係数パス #

正則化係数 α を変えると各特徴量の係数がどう収縮するか確認できます。

まとめ #

  • リッジ回帰はL2正則化で係数を滑らかに縮小し、多重共線性があっても安定した推定を行います。
  • ラッソ回帰はL1正則化で不要な係数を0にし、特徴量選択とモデルの解釈性向上に役立ちます。
  • 正則化強度\(\alpha\)はRidgeCV/LassoCVで交差検証により自動選択するのが実務的です。
  • 標準化は必須の前処理であり、パイプラインに組み込んで使用してください。

参考文献 #

  • Hoerl, A. E., & Kennard, R. W. (1970). Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, 12(1), 55–67.
  • Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society: Series B, 58(1), 267–288.
  • Zou, H., & Hastie, T. (2005). Regularization and Variable Selection via the Elastic Net. Journal of the Royal Statistical Society: Series B, 67(2), 301–320.