2.3.3
決定木のパラメータ
まとめ
- 決定木は深く成長させるほど訓練データへの当てはまりが良くなる一方で、過学習のリスクが高まる。
max_depthやmin_samples_leafなどのハイパーパラメータは木の複雑さを抑えるブレーキとして機能する。- コスト複雑度剪定(
ccp_alpha)は訓練誤差と木のサイズのトレードオフを明示的に最適化するアプローチである。 - パラメータを変えたときの決定境界や予測面を可視化すると、モデル挙動とパラメータの関係を直感的に把握できる。
- 決定木分類器 の概念を先に学ぶと理解がスムーズです
直感 #
決定木は「もし◯◯なら左へ、そうでなければ右へ」と条件を繰り返し、葉ノードで値を返します。制限を設けなければ訓練データをほぼ完璧に近似できますが、そのぶんデータのわずかな揺らぎにも敏感になります。max_depth や min_samples_leaf といったパラメータを調整し、木の成長を適度に抑えることで汎化性能を確保することが重要です。
具体的な数式 #
親ノード \(P\) を左右の子ノード \(L, R\) に分割したときの不純度減少量は
$$ \Delta I = I(P) - \frac{|L|}{|P|} I(L) - \frac{|R|}{|P|} I(R) $$で表されます。回帰木の場合、\(I(t)\) を平均二乗誤差や平均絶対誤差として定義し、\(\Delta I\) が最大となる特徴量としきい値を選びます。
剪定では木 \(T\) のコスト複雑度
$$ R_\alpha(T) = R(T) + \alpha |T| $$を最小化する部分木を探します。ここで \(R(T)\) は訓練誤差、\(|T|\) は葉ノード数、\(\alpha \ge 0\) は複雑さへのペナルティを表します。
Pythonを用いた実験や説明 #
以下は 2 次元回帰データに対して異なるパラメータ設定を試すシンプルな例です。max_depth、ccp_alpha、min_samples_leaf を切り替えると、同じデータでも予測面が大きく変化することが分かります。
| |
可視化ギャラリー #
以下の画像は過去に作成したノートブックを再利用したもので、パラメータ設定を変えたときの決定境界や予測面の違いをまとめています。
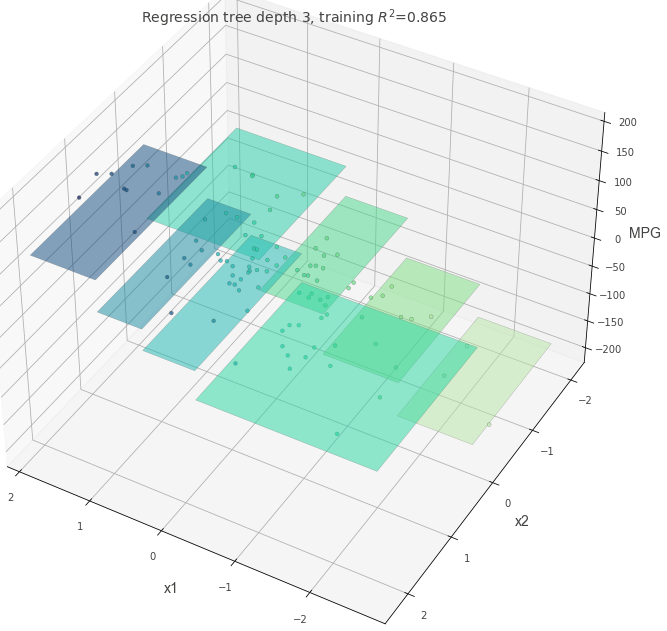
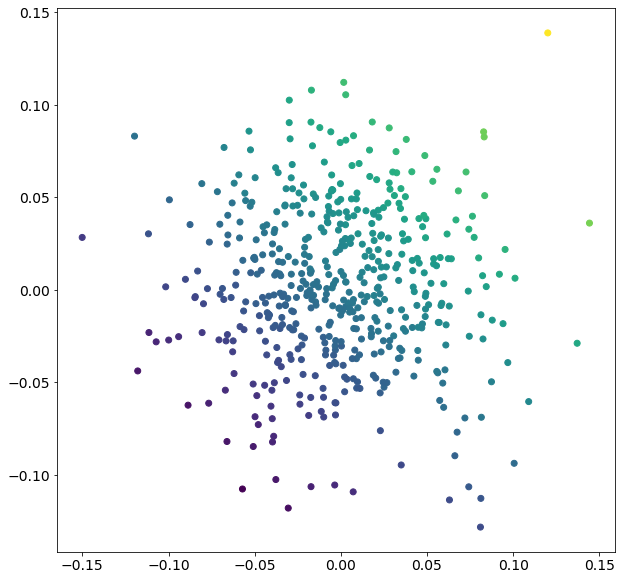
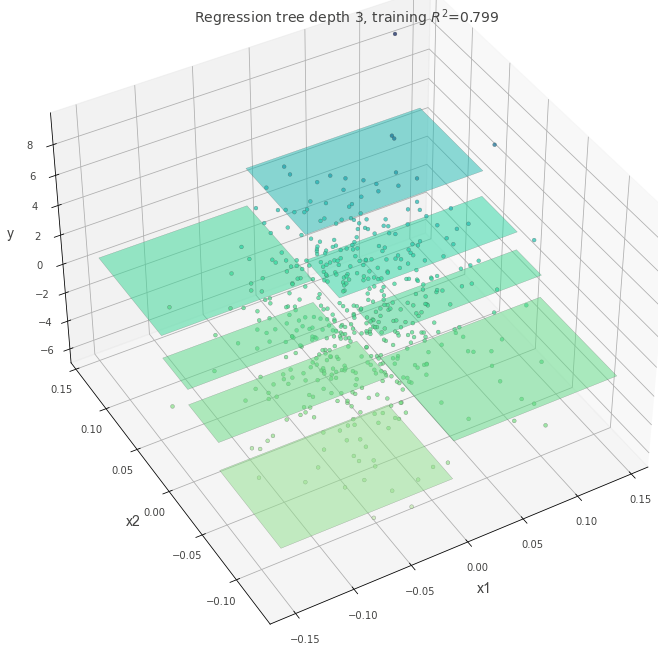

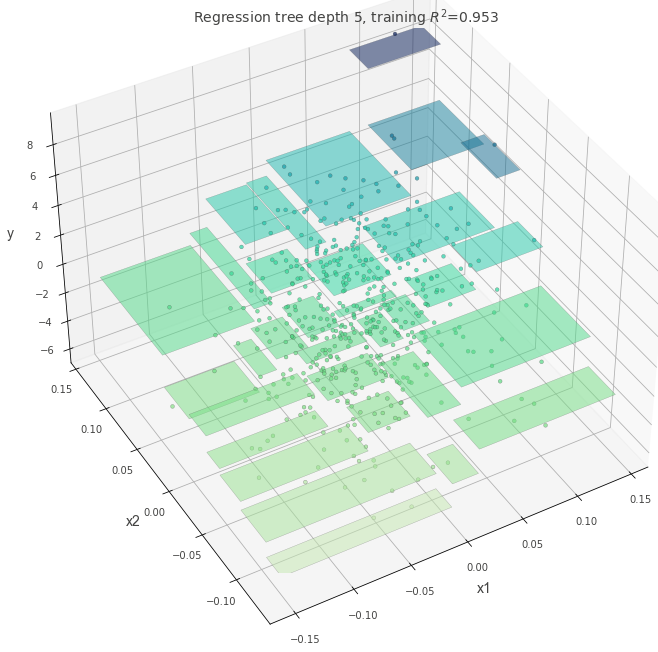
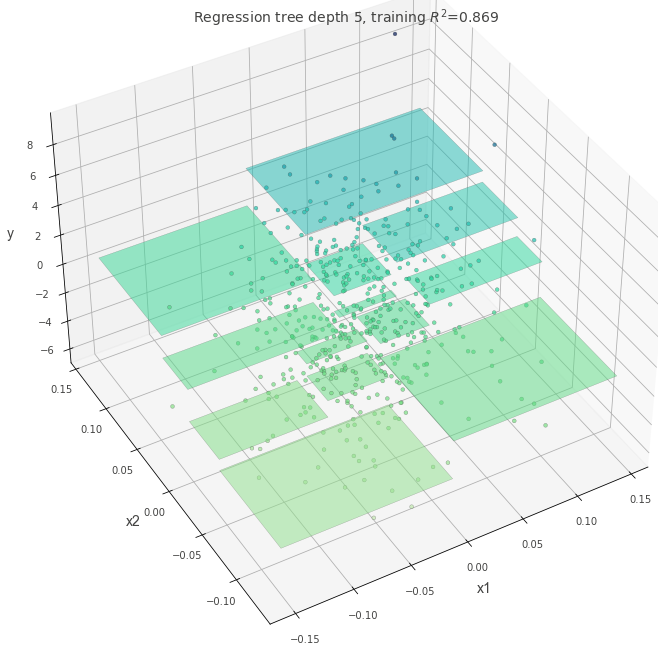
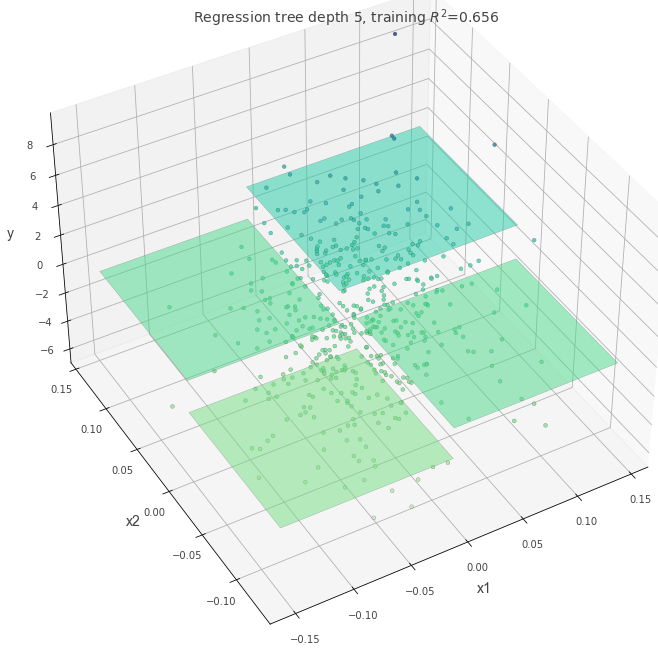
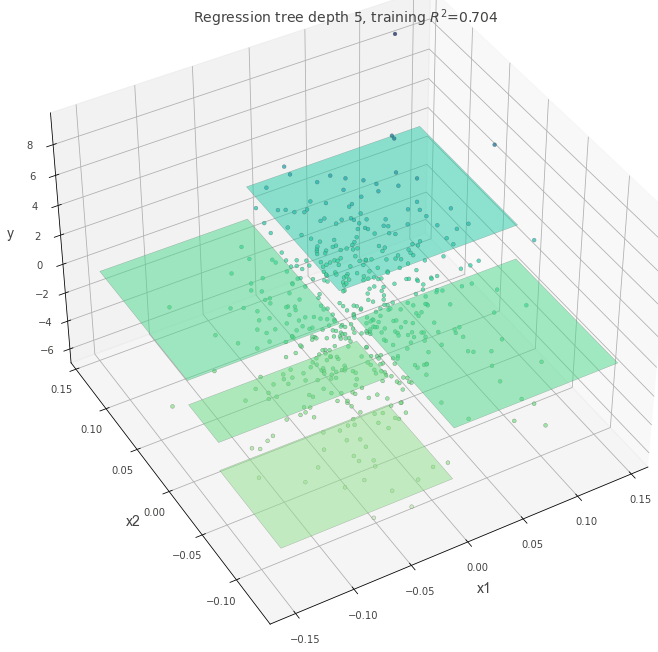

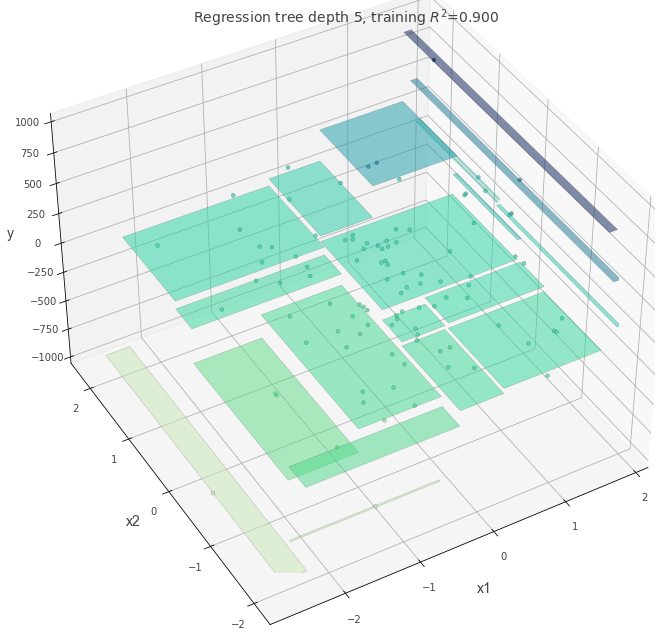
深さとモデルの複雑さ #
最大深さを変えると訓練精度とテスト精度がどう乖離するか確認できます。
参考文献 #
- Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
- Breiman, L., & Friedman, J. H. (1991). Cost-Complexity Pruning. In Classification and Regression Trees. Chapman & Hall.
- scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html