Logistic Regression
Logistic regression is a model for two-class classification. This method try to convert the numerical values output by the linear regression model into probabilities so that the classification problem can be solved. On this page, I will run the logistic regression implemented in sikit-learn and draw its decision boundary (the boundary on which the classification is based).
import matplotlib.pyplot as plt
import numpy as np
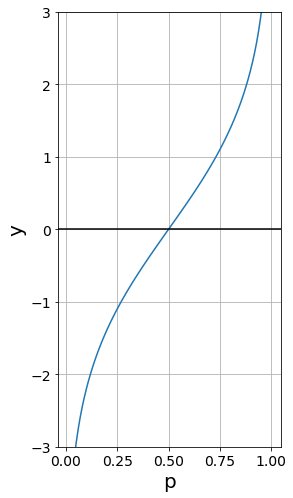
Visualization of Logit Functions
fig = plt.figure(figsize=(4, 8))
p = np.linspace(0.01, 0.999, num=100)
y = np.log(p / (1 - p))
plt.plot(p, y)
plt.xlabel("p")
plt.ylabel("y")
plt.axhline(y=0, color="k")
plt.ylim(-3, 3)
plt.grid()
plt.show()
Logistic Regression
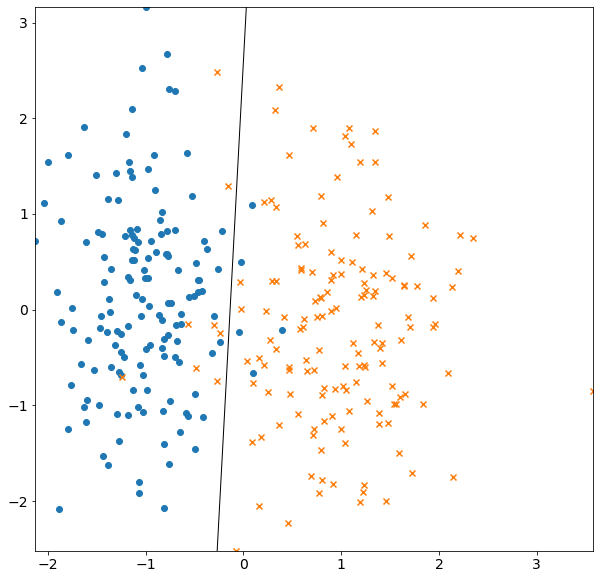
In this section, I try to train Logistic regression on artificially generated data.
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import make_classification
## Dataset
X, Y = make_classification(
n_samples=300,
n_features=2,
n_redundant=0,
n_informative=1,
random_state=2,
n_clusters_per_class=1,
)
# Training LogisticRegression
clf = LogisticRegression()
clf.fit(X, Y)
# Find the decision boundary
b = clf.intercept_[0]
w1, w2 = clf.coef_.T
b_1 = -w1 / w2
b_0 = -b / w2
xmin, xmax = np.min(X[:, 0]), np.max(X[:, 0])
ymin, ymax = np.min(X[:, 1]), np.max(X[:, 1])
xd = np.array([xmin, xmax])
yd = b_1 * xd + b_0
# Plot Graphs
plt.figure(figsize=(10, 10))
plt.plot(xd, yd, "k", lw=1, ls="-")
plt.scatter(*X[Y == 0].T, marker="o")
plt.scatter(*X[Y == 1].T, marker="x")
plt.xlim(xmin, xmax)
plt.ylim(ymin, ymax)
plt.show()