Softmax Regression

Last updated 2020-02-12 Read time 3 min

Summary

Softmax regression generalises logistic regression to multiple classes, producing the probability of every class simultaneously.
Outputs lie in $[0, 1]$ and sum to 1, so they plug directly into decision thresholds, cost-sensitive rules, or downstream pipelines.
Training minimises the cross-entropy loss, directly correcting discrepancies between predicted and true probability distributions.
In scikit-learn, LogisticRegression(multi_class="multinomial") implements softmax regression and supports L1/L2 regularisation.

Logistic Regression — understanding this concept first will make learning smoother

Intuition #

This method should be interpreted through its assumptions, data conditions, and how parameter choices affect generalization.

Detailed Explanation #

Mathematical formulation #

Let $K$ be the number of classes, $\mathbf{w}_k$ and $b_k$ the parameters for class $k$. Then

$$ P(y = k \mid \mathbf{x}) = \frac{\exp\left(\mathbf{w}_k^\top \mathbf{x} + b_k\right)} {\sum_{j=1}^{K} \exp\left(\mathbf{w}_j^\top \mathbf{x} + b_j\right)}. $$

The objective is the cross-entropy loss

$$ L = - \sum_{i=1}^{n} \sum_{k=1}^{K} \mathbb{1}(y_i = k) \log P(y = k \mid \mathbf{x}_i), $$

with optional regularisation on the weights to prevent overfitting.

Experiments with Python #

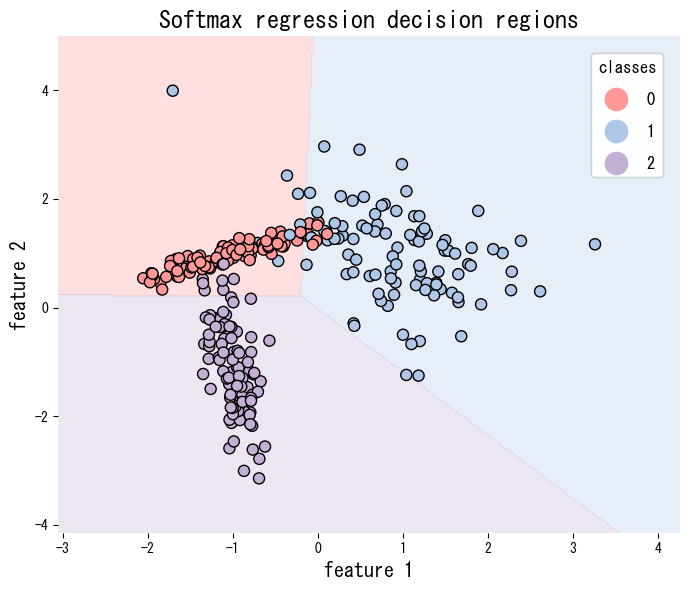
The script below applies softmax regression to a synthetic three-class data set and visualises the decision regions. Setting multi_class="multinomial" activates the softmax formulation.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.colors import ListedColormap
from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score

def run_softmax_regression_demo(
    n_samples: int = 300,
    n_classes: int = 3,
    random_state: int = 42,
    label_title: str = "Softmax regression decision regions",
    xlabel: str = "feature 1",
    ylabel: str = "feature 2",
) -> dict[str, float]:
    """Train a softmax regression model and visualise decision regions."""
    japanize_matplotlib.japanize()
    X, y = make_classification(
        n_samples=n_samples,
        n_features=2,
        n_informative=2,
        n_redundant=0,
        n_clusters_per_class=1,
        n_classes=n_classes,
        random_state=random_state,
    )

    clf = LogisticRegression(multi_class="multinomial", solver="lbfgs")
    clf.fit(X, y)

    accuracy = float(accuracy_score(y, clf.predict(X)))

    x1_min, x1_max = X[:, 0].min() - 1.0, X[:, 0].max() + 1.0
    x2_min, x2_max = X[:, 1].min() - 1.0, X[:, 1].max() + 1.0
    grid_x1, grid_x2 = np.meshgrid(
        np.linspace(x1_min, x1_max, 400),
        np.linspace(x2_min, x2_max, 400),
    )
    grid_points = np.c_[grid_x1.ravel(), grid_x2.ravel()]
    preds = clf.predict(grid_points).reshape(grid_x1.shape)

    cmap = ListedColormap(["#ff9896", "#98df8a", "#aec7e8", "#f7b6d2", "#c5b0d5"])
    fig, ax = plt.subplots(figsize=(7, 6))
    ax.contourf(grid_x1, grid_x2, preds, alpha=0.3, cmap=cmap, levels=np.arange(-0.5, n_classes + 0.5, 1))
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolor="k", cmap=cmap)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_title(label_title)
    legend = ax.legend(*scatter.legend_elements(), title="classes", loc="best")
    ax.add_artist(legend)
    fig.tight_layout()
    plt.show()

    return {"accuracy": accuracy}

metrics = run_softmax_regression_demo(
    label_title="Softmax regression decision regions",
    xlabel="feature 1",
    ylabel="feature 2",
)
print(f"Training accuracy: {metrics['accuracy']:.3f}")

Setting multi_class=“multinomial” activates the softmax form… figure

References #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.