DBSCAN | Density-based clustering with noise handling

まとめ

DBSCAN (Density-Based Spatial Clustering of Applications with Noise) groups points according to local density so clusters can take any shape while sparse regions become noise.
Two hyperparameters control the model: eps, the neighbourhood radius, and min_samples, the minimum number of neighbours required for a point to become a core sample.
Points are labelled core, border, or noise; clusters are connected components of core points plus their border neighbours.
A common tuning recipe is to fix min_samples (≥ dimensionality + 1) and sweep eps while inspecting the share of points flagged as noise.

1. Overview #

DBSCAN does not require the number of clusters beforehand. Instead, it inspects each sample:

Core points: at least min_samples neighbours within distance eps.
Border points: lie within the eps-ball of a core point but fail the core criterion themselves.
Noise points: belong to no core neighbourhood.

Because of this density view, DBSCAN is robust to non-convex clusters such as two moons or concentric circles. Always scale the features so eps has a meaningful interpretation.

2. Formal definition #

Given (x_i \in \mathcal{X}), its (\varepsilon)-neighbourhood is

$$ \mathcal{N}_\varepsilon(x_i) = { x_j \in \mathcal{X} \mid \lVert x_i - x_j \rVert \le \varepsilon }. $$

If (|\mathcal{N}_\varepsilon(x_i)| \ge \texttt{min_samples}|), the point is core. DBSCAN builds clusters by exploring density-reachable points; anything left unvisited becomes noise. With a spatial index the overall complexity is (O(n \log n)).

3. Python example #

The snippet below uses scikit-learn’s DBSCAN on a two-moons dataset, colours core/border points differently, and reports how many samples are marked as noise.

from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from numpy.typing import NDArray
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler


def run_dbscan_demo(
    n_samples: int = 600,
    noise: float = 0.08,
    eps: float = 0.3,
    min_samples: int = 10,
    random_state: int = 0,
) -> dict[str, int]:
    japanize_matplotlib.japanize()
    features, _ = make_moons(
        n_samples=n_samples,
        noise=noise,
        random_state=random_state,
    )
    features = StandardScaler().fit_transform(features)

    model = DBSCAN(eps=eps, min_samples=min_samples)
    labels = model.fit_predict(features)

    unique_labels = sorted(np.unique(labels))
    cluster_ids = [label for label in unique_labels if label != -1]
    noise_count = int(np.sum(labels == -1))

    core_mask = np.zeros(labels.shape[0], dtype=bool)
    if hasattr(model, "core_sample_indices_"):
        core_mask[model.core_sample_indices_] = True

    fig, ax = plt.subplots(figsize=(6.2, 5.2))
    palette = plt.cm.get_cmap("tab10", max(len(cluster_ids), 1))

    for order, cluster_id in enumerate(cluster_ids):
        mask = labels == cluster_id
        color = palette(order)
        ax.scatter(
            features[mask & core_mask, 0],
            features[mask & core_mask, 1],
            c=[color],
            s=36,
            edgecolor="white",
            linewidth=0.2,
            label=f"Cluster {cluster_id} core",
        )
        ax.scatter(
            features[mask & ~core_mask, 0],
            features[mask & ~core_mask, 1],
            c=[color],
            s=24,
            edgecolor="white",
            linewidth=0.2,
            marker="o",
            label=f"Cluster {cluster_id} border",
        )

    if noise_count:
        noise_mask = labels == -1
        ax.scatter(
            features[noise_mask, 0],
            features[noise_mask, 1],
            c="#9ca3af",
            marker="x",
            s=28,
            linewidth=0.8,
            label="Noise",
        )

    ax.set_title("DBSCAN clustering demo")
    ax.set_xlabel("Feature 1")
    ax.set_ylabel("Feature 2")
    ax.grid(alpha=0.2)
    ax.legend(loc="upper right", fontsize=9)
    fig.tight_layout()
    plt.show()

    return {"n_clusters": len(cluster_ids), "n_noise": noise_count}


result = run_dbscan_demo()
print(f"Clusters discovered: {result['n_clusters']}")
print(f"Noise points: {result['n_noise']}")

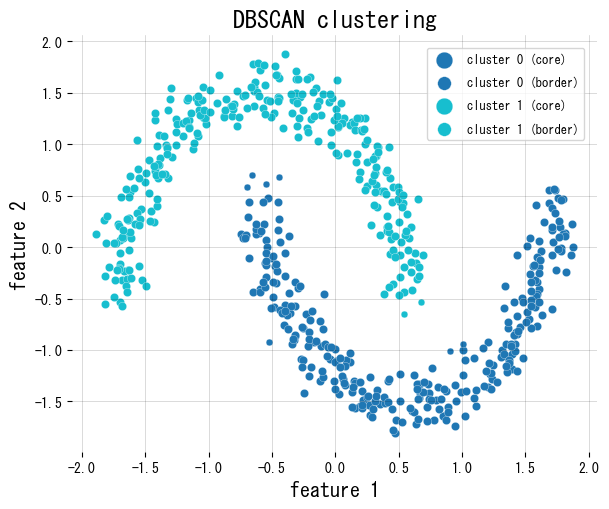
DBSCAN clustering result

4. Practical tips #

Plot the sorted distances to the k-th neighbour (k = min_samples) to pick eps where the curve exhibits an elbow.
Use pipelines so standardisation and clustering run together; otherwise distance-based decisions become meaningless.
For very large datasets consider approximate nearest neighbours or switch to HDBSCAN, which extends DBSCAN to multi-density data and removes the need to tune eps.

5. References #

Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. KDD.
Schubert, E., Sander, J., Ester, M., Kriegel, H.-P., & Xu, X. (2017). DBSCAN Revisited, Revisited. ACM Transactions on Database Systems.
scikit-learn developers. (2024). Clustering. https://scikit-learn.org/stable/modules/clustering.html