k-means++
k-means is a type of clustering algorithm. In order to group the given data into k clusters, the average of each cluster is computed ↔ the data is repeatedly assigned to the nearest representative point. k-means varies in the way it converges depending on the initial value of the k representative points. The convergence of k-means depends on the initial values of k representative points. k-means++ can be used to obtain more stable results by taking the initial values in a different way.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
Comparing clustering results between k-means++ and k-means(random initial value selection)
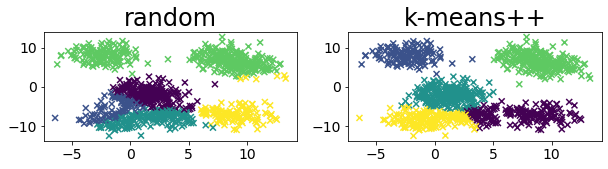
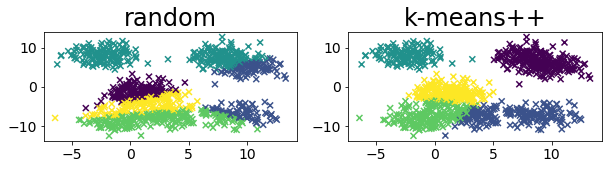
Compare the clustering results between random and kmeans++.
You can see that k-means++ may split the upper left cluster into two clusters.
*In this example, we dare to specify max_iter=1.
n_samples = 3000
random_state = 11711
X, y = make_blobs(
n_samples=n_samples, random_state=random_state, cluster_std=1.5, centers=8
)
plt.figure(figsize=(8, 8))
for i in range(10):
# Compare k-means and k-means++
rand_index = np.random.permutation(1000)
X_rand = X[rand_index]
y_pred_rnd = KMeans(
n_clusters=5, random_state=random_state, init="random", max_iter=1, n_init=1
).fit_predict(X_rand)
y_pred_kpp = KMeans(
n_clusters=5, random_state=random_state, init="k-means++", max_iter=1, n_init=1
).fit_predict(X_rand)
plt.figure(figsize=(10, 2))
plt.subplot(1, 2, 1)
plt.title(f"random")
plt.scatter(X_rand[:, 0], X_rand[:, 1], c=y_pred_rnd, marker="x")
plt.subplot(1, 2, 2)
plt.title(f"k-means++")
plt.scatter(X_rand[:, 0], X_rand[:, 1], c=y_pred_kpp, marker="x")
plt.show()
plt.tight_layout()
plt.show()