Least-squares method
The least-squares method refers to finding the coefficients of a function to minimize the sum of squares of the residuals when fitting a function to a collection of pairs of numbers $(x_i, y_i)$ in order to know their relationship. In this page, we will try to perform the least-squares method on sample data using scikit-learn.
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
japanize_matplotlib is imported to display Japanese in the graph.
Create regression data for experiments
Use np.linspace to create data. It creates a list of values equally spaced between the values you specify. The following code creates 500 sample data for linear regression.
# Training data
n_samples = 500
X = np.linspace(-10, 10, n_samples)[:, np.newaxis]
epsolon = np.random.normal(size=n_samples)
y = np.linspace(-2, 2, n_samples) + epsolon
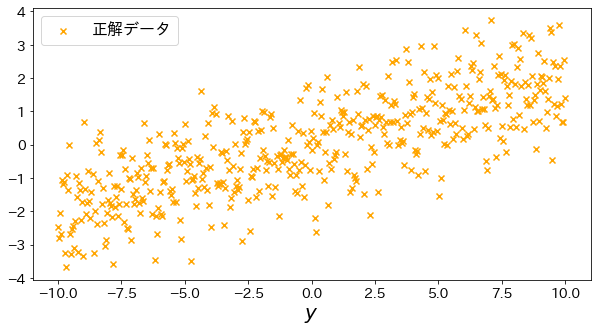
# Visualize straight lines
plt.figure(figsize=(10, 5))
plt.scatter(X, y, marker="x", label="Target", c="orange")
plt.xlabel("$x_1$")
plt.xlabel("$y$")
plt.legend()
plt.show()
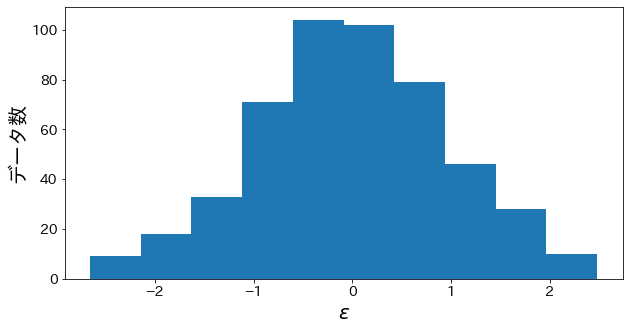
Check noise on y
About y = np.linspace(-2, 2, n_samples) + epsolon, I plot a histogram for epsolon.
Confirm that noise with a distribution close to the normal distribution is on the target variable.
plt.figure(figsize=(10, 5))
plt.hist(epsolon)
plt.xlabel("$\epsilon$")
plt.ylabel("#data")
plt.show()
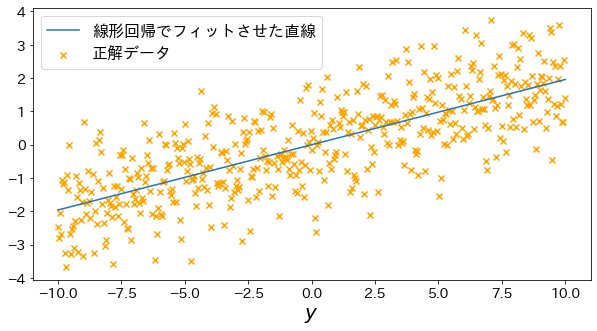
Fit a straight line by the least-squares method
# fit your model
lin_r = make_pipeline(StandardScaler(with_mean=False), LinearRegression()).fit(X, y)
y_pred = lin_r.predict(X)
# Visualize straight lines
plt.figure(figsize=(10, 5))
plt.scatter(X, y, marker="x", label="target", c="orange")
plt.plot(X, y_pred, label="Straight line fitted by linear regression")
plt.xlabel("$x_1$")
plt.xlabel("$y$")
plt.legend()
plt.show()