Quantile Regression

Last updated 2020-04-22 Read time 3 min

Summary

Quantile regression directly estimates arbitrary quantiles—such as the median or the 10th percentile—instead of only the mean.
Minimizing the pinball loss yields robustness to outliers and accommodates asymmetric noise.
Independent models can be fit for different quantiles, and stacking them forms prediction intervals.
Feature scaling and regularization help stabilize convergence and maintain generalization.

Intuition #

This method should be interpreted through its assumptions, data conditions, and how parameter choices affect generalization.

Detailed Explanation #

Mathematical formulation #

With residual $r = y - \hat{y}$ and quantile level $\tau \in (0, 1)$, the pinball loss is defined as

$$ L_\tau(r) = \begin{cases} \tau r & (r \ge 0) \\ (\tau - 1) r & (r < 0) \end{cases} $$

Minimizing this loss yields a linear predictor for the $\tau$-quantile. Setting $\tau = 0.5$ recovers the median and leads to the same solution as least absolute deviations regression.

Experiments with Python #

We use QuantileRegressor to estimate the 0.1, 0.5, and 0.9 quantiles and compare them with ordinary least squares.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression, QuantileRegressor
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

def run_quantile_regression_demo(
    taus: tuple[float, ...] = (0.1, 0.5, 0.9),
    n_samples: int = 400,
    xlabel: str = "input x",
    ylabel: str = "output y",
    label_observations: str = "observations",
    label_mean: str = "mean (OLS)",
    label_template: str = "quantile τ={tau}",
    title: str | None = None,
) -> dict[float, tuple[float, float]]:
    """Fit quantile regressors alongside OLS and plot the conditional bands.

    Args:
        taus: Quantile levels to fit (each in (0, 1)).
        n_samples: Number of synthetic observations to generate.
        xlabel: Label for the x-axis.
        ylabel: Label for the y-axis.
        label_observations: Legend label for the scatter plot.
        label_mean: Legend label for the OLS line.
        label_template: Format string for quantile labels.
        title: Optional title for the plot.

    Returns:
        Mapping of quantile level to (min prediction, max prediction).
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(123)

    x_values: np.ndarray = np.linspace(0.0, 10.0, n_samples, dtype=float)
    noise: np.ndarray = rng.gamma(shape=2.0, scale=1.0, size=n_samples) - 2.0
    y_values: np.ndarray = 1.5 * x_values + 5.0 + noise
    X: np.ndarray = x_values[:, np.newaxis]

    quantile_models: dict[float, make_pipeline] = {}
    for tau in taus:
        model = make_pipeline(
            StandardScaler(with_mean=True),
            QuantileRegressor(alpha=0.001, quantile=float(tau), solver="highs"),
        )
        model.fit(X, y_values)
        quantile_models[tau] = model

    ols = LinearRegression()
    ols.fit(X, y_values)

    grid: np.ndarray = np.linspace(0.0, 10.0, 200, dtype=float)[:, np.newaxis]
    preds = {tau: model.predict(grid) for tau, model in quantile_models.items()}
    ols_pred: np.ndarray = ols.predict(grid)

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y_values, s=15, alpha=0.4, label=label_observations)

    color_cycle = plt.rcParams["axes.prop_cycle"].by_key().get("color", ["#1f77b4", "#ff7f0e", "#2ca02c"])
    for idx, tau in enumerate(taus):
        color = color_cycle[idx % len(color_cycle)]
        ax.plot(
            grid,
            preds[tau],
            color=color,
            linewidth=2,
            label=label_template.format(tau=tau),
        )

    ax.plot(grid, ols_pred, color="#9467bd", linestyle="--", label=label_mean)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    summary: dict[float, tuple[float, float]] = {
        tau: (float(pred.min()), float(pred.max())) for tau, pred in preds.items()
    }
    return summary

summary = run_quantile_regression_demo()
for tau, (ymin, ymax) in summary.items():
    print(f"tau={tau:.1f}: min prediction {ymin:.2f}, max prediction {ymax:.2f}")

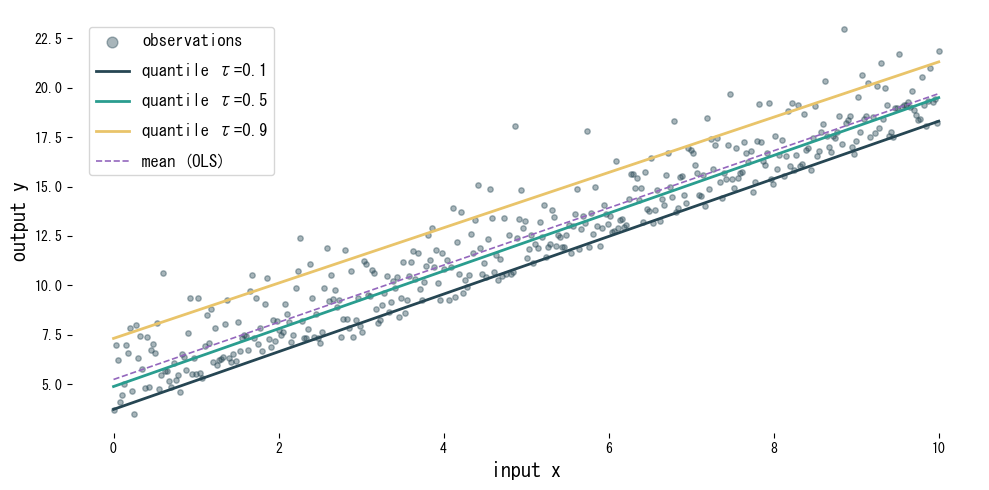
9 quantiles and compare them with ordinary least squares figure

Reading the results #

Each quantile produces a different line, capturing the vertical spread of the data.
Compared with the mean-focused OLS model, quantile regression adapts to skewed noise.
Combining multiple quantiles yields prediction intervals that communicate decision-relevant uncertainty.

References #

Koenker, R., & Bassett, G. (1978). Regression Quantiles. Econometrica, 46(1), 33–50.
Koenker, R. (2005). Quantile Regression. Cambridge University Press.