Outliers and Robustness
Outlier is a general term for a value that is anomalous (very large or conversely small) compared to other values. What values are outliers depends on the problem setting and the nature of the data. On this page, we will review the difference in results between "regression with squared error" and "regression with Huber loss" for data with outliers.
import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
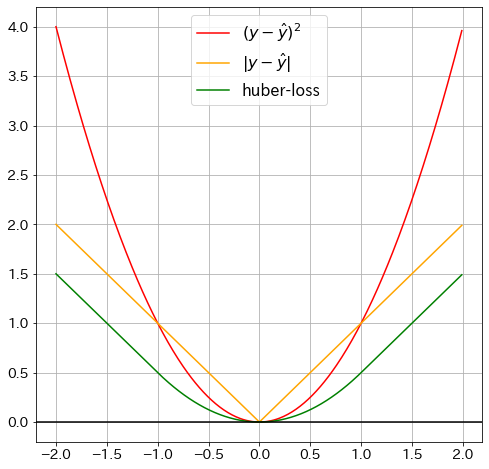
Visualisation of Huber loss
def huber_loss(y_pred: float, y: float, delta=1.0):
"""HuberLoss"""
huber_1 = 0.5 * (y - y_pred) ** 2
huber_2 = delta * (np.abs(y - y_pred) - 0.5 * delta)
return np.where(np.abs(y - y_pred) <= delta, huber_1, huber_2)
delta = 1.5
x_vals = np.arange(-2, 2, 0.01)
y_vals = np.where(
np.abs(x_vals) <= delta,
0.5 * np.square(x_vals),
delta * (np.abs(x_vals) - 0.5 * delta),
)
# plot graph
fig = plt.figure(figsize=(8, 8))
plt.plot(x_vals, x_vals ** 2, "red", label=r"$(y-\hat{y})^2$") ## Squared error
plt.plot(x_vals, np.abs(x_vals), "orange", label=r"$|y-\hat{y}|$") ## Absolute error
plt.plot(
x_vals, huber_loss(x_vals * 2, x_vals), "green", label=r"huber-loss"
) # Huber-loss
plt.axhline(y=0, color="k")
plt.grid(True)
plt.legend()
plt.show()
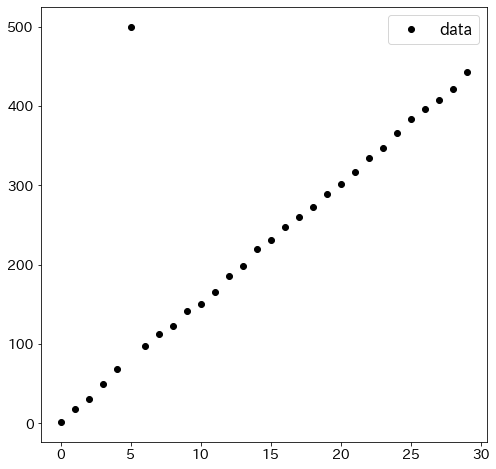
Comparison with the least-squares method
Prepare data for the experiment
To compare regression with Huber loss and normal linear regression, one outlier is intentionally included in the data.
N = 30
x1 = np.array([i for i in range(N)])
x2 = np.array([i for i in range(N)])
X = np.array([x1, x2]).T
epsilon = np.array([np.random.random() for i in range(N)])
y = 5 * x1 + 10 * x2 + epsilon * 10
y[5] = 500
plt.figure(figsize=(8, 8))
plt.plot(x1, y, "ko", label="data")
plt.legend()
plt.show()
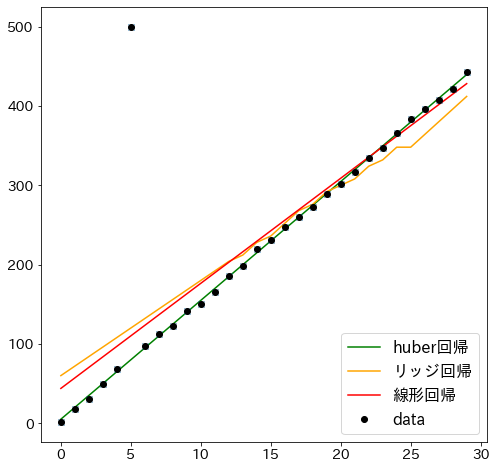
Compare with least squares, ridge regression and huber regression
from sklearn.datasets import make_regression
from sklearn.linear_model import HuberRegressor, Ridge
from sklearn.linear_model import LinearRegression
plt.figure(figsize=(8, 8))
huber = HuberRegressor(alpha=0.0, epsilon=3)
huber.fit(X, y)
plt.plot(x1, huber.predict(X), "green", label="huber regression")
ridge = Ridge(alpha=0.0, random_state=0)
ridge.fit(X, y)
plt.plot(x1, ridge.predict(X), "orange", label="ridge regression")
lr = LinearRegression()
lr.fit(X, y)
plt.plot(x1, lr.predict(X), "r-", label="least square regression")
plt.plot(x1, y, "x")
plt.plot(x1, y, "ko", label="data")
plt.legend()
plt.show()