Decision Tree Classifier | Splitting Data with Information Gain

1. Overview #

Decision trees are supervised learning models that recursively split the input space. Starting from the root, each internal node asks a question like “is (x_j \le s)?” and routes the sample to the next node. For classification we want leaves that are as pure as possible, meaning they contain almost only one class label. The final model is therefore a compact rule book that can easily be inspected or converted into business logic.

2. Impurity measures #

Let (t) be a node and (p_k) the class proportion inside that node. Two common impurity scores are

$$ \mathrm{Gini}(t) = 1 - \sum_k p_k^2, $$

$$ H(t) = - \sum_k p_k \log p_k. $$

When splitting node (t) on feature (x_j) with threshold (s), we evaluate the gain

$$ \Delta I = I(t) - \frac{n_L}{n_t} I(t_L) - \frac{n_R}{n_t} I(t_R), $$

where (I(\cdot)) is either Gini or entropy, (t_L) and (t_R) are the child nodes, and (n_t) is the number of samples reaching (t). The split that maximises (\Delta I) is selected.

3. Python example #

The snippet below generates a two-class toy dataset with make_classification, fits a DecisionTreeClassifier, and visualises its decision regions. Changing criterion from "gini" to "entropy" switches the impurity measure.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier, plot_tree

n_classes = 2
X, y = make_classification(
    n_samples=100,
    n_features=2,
    n_redundant=0,
    n_informative=2,
    random_state=2,
    n_classes=n_classes,
    n_clusters_per_class=1,
)

clf = DecisionTreeClassifier(criterion="gini", random_state=0).fit(X, y)

x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(
    np.arange(x_min, x_max, 0.1),
    np.arange(y_min, y_max, 0.1),
)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

plt.figure(figsize=(8, 8))
plt.contourf(xx, yy, Z, cmap=plt.cm.Pastel1, alpha=0.6)
plt.xlabel("x1")
plt.ylabel("x2")
for i, color, label_name in zip(range(n_classes), ["r", "b"], ["A", "B"]):
    idx = np.where(y == i)
    plt.scatter(X[idx, 0], X[idx, 1], c=color, label=label_name, edgecolor="k")
plt.legend()
plt.title("Decision regions created by a tree")
plt.show()

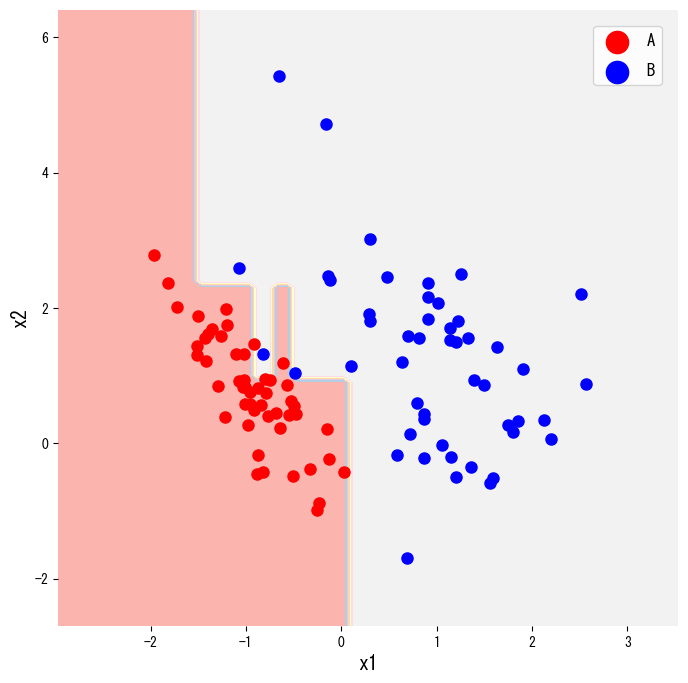
The same estimator can be rendered as an actual tree diagram with plot_tree, which is convenient for reports or slide decks.

plt.figure(figsize=(12, 12))
plot_tree(clf, filled=True, feature_names=["x1", "x2"], class_names=["A", "B"])
plt.show()

4. References #