Decision Tree (Regressor)

Last updated 2025-11-05 Read time 3 min

Summary

Regression trees approximate nonlinear relationships by recursively splitting the feature space until each leaf can be represented by a single constant value.
Splits minimise the mean squared error (MSE) of the left and right children; the reduction in MSE determines whether a question is useful.
Hyperparameters such as max_depth, min_samples_leaf, and ccp_alpha balance accuracy against interpretability and help avoid overfitting.
Visual diagnostics—scatter plots, contour maps, and rendered trees—make it easy to explain which regions share the same prediction.

Decision Tree Classifier — understanding this concept first will make learning smoother

Intuition #

This method should be interpreted through its assumptions, data conditions, and how parameter choices affect generalization.

Detailed Explanation #

1. Overview #

Like classifiers, regression trees ask simple questions about the input features, but the target is continuous. Each leaf predicts a constant (the average of training samples that arrived there). Because the function is piecewise constant, increasing depth captures increasingly fine-grained structure, while shallow trees emphasise smooth trends.

2. Split criterion (variance reduction) #

For a node (t) containing (n_t) samples and average target (\bar{y}_t), the impurity is the node MSE:

$$ \mathrm{MSE}(t) = \frac{1}{n_t} \sum_{i \in t} (y_i - \bar{y}_t)^2. $$

Splitting on (x_j) at threshold (s) yields children (t_L) and (t_R). The quality of the split is measured by

$$ \Delta = \mathrm{MSE}(t) - \frac{n_L}{n_t} \mathrm{MSE}(t_L) - \frac{n_R}{n_t} \mathrm{MSE}(t_R). $$

We choose the split with the largest (\Delta); when no split yields positive gain, the node becomes a leaf.

3. Python example #

The first snippet fits a shallow tree to noisy samples drawn from a sine curve so we can see the piecewise-constant nature of the prediction. A second experiment trains a two-feature regressor, evaluates (R^2), RMSE, and MAE, and visualises the learned surface plus the final tree.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

rng = np.random.default_rng(42)
X1 = np.sort(5 * rng.random((120, 1)), axis=0)
y1_true = np.sin(X1).ravel()
y1 = y1_true + rng.normal(scale=0.2, size=X1.shape[0])

reg1 = DecisionTreeRegressor(max_depth=3, random_state=0).fit(X1, y1)
y1_pred = reg1.predict(X1)

plt.figure(figsize=(8, 4))
plt.scatter(X1, y1, s=15, c="gray", label="observations")
plt.plot(X1, y1_true, lw=2, label="true signal")
plt.step(X1.ravel(), y1_pred, where="mid", lw=2, label="tree prediction")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Piecewise-constant fit by a regression tree")
plt.legend()
plt.grid(alpha=0.3)
plt.show()

Tree fit on a 1D sine curve

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
X, y = make_regression(n_samples=400, n_features=2, noise=15.0, random_state=777)
reg = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)

r2 = r2_score(y, reg.predict(X))
rmse = mean_squared_error(y, reg.predict(X), squared=False)
mae = mean_absolute_error(y, reg.predict(X))
print(f"R2={r2:.3f}  RMSE={rmse:.2f}  MAE={mae:.2f}")

x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(
    np.linspace(x_min, x_max, 150),
    np.linspace(y_min, y_max, 150),
)
zz = reg.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)

plt.figure(figsize=(7, 6))
cs = plt.contourf(xx, yy, zz, levels=15, cmap="viridis", alpha=0.8)
plt.colorbar(cs, label="prediction")
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis", s=20, edgecolor="k", alpha=0.7)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Prediction surface of the regression tree")
plt.show()

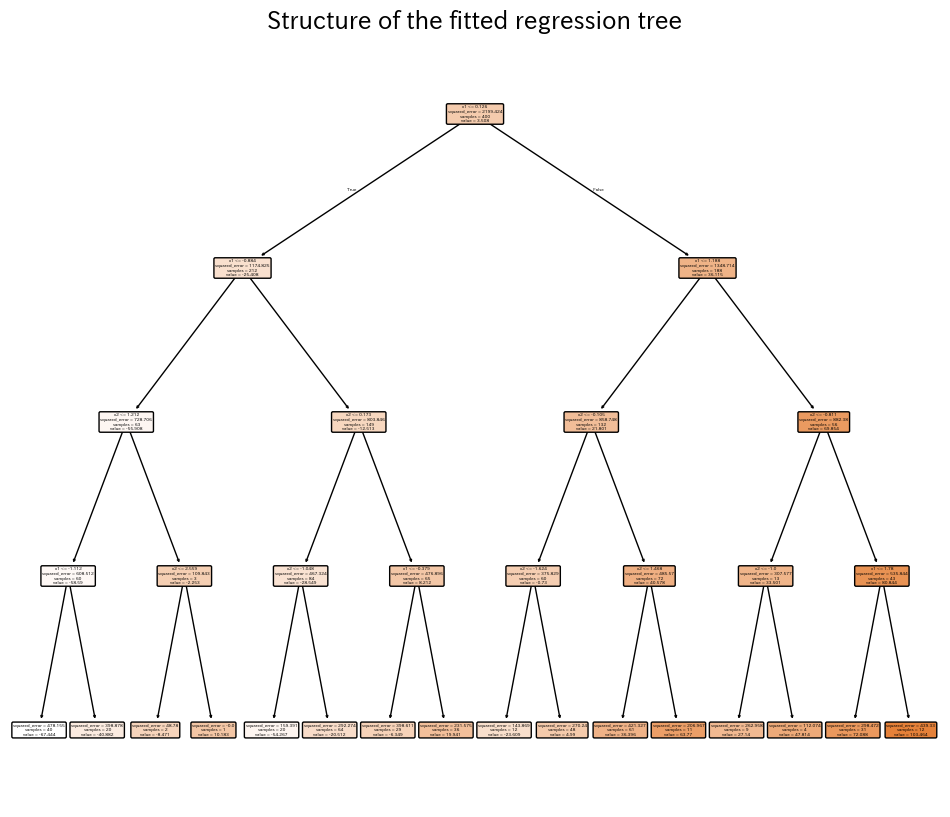
Prediction surface of the regression tree

1
2
3
4
5
6
7
8
9
plt.figure(figsize=(12, 10))
plot_tree(
    reg,
    filled=True,
    feature_names=["x1", "x2"],
    rounded=True,
)
plt.title("Structure of the fitted regression tree")
plt.show()

Rendered tree structure

4. References #

Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html