Stratified k-fold cross-validation

Last updated 2020-02-12 Read time 2 min

Summary

Stratified k-fold preserves class proportions in every fold, which is essential for imbalanced datasets.
Compare stratified and standard k-fold to visualise how class bias differs between them.
Review design tips for extreme imbalance scenarios and how to interpret the results in practice.

Cross-Validation — understanding this concept first will make learning smoother

sklearn.model_selection.StratifiedKFold

1
2
3
4
5
6
7
8
9
import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib
from sklearn.datasets import make_classification
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import KFold, StratifiedKFold, train_test_split
from sklearn.metrics import roc_auc_score

RND = 42

Building a model and running cross-validation #

Experimental dataset #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
n_classes = 10
X, y = make_classification(
    n_samples=210,
    n_classes=n_classes,
    n_informative=n_classes,
    n_features=12,
    n_clusters_per_class=1,
    weights=[0.82, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02, 0.02],
    random_state=RND,
)
plt.title("Samples per class in y")
plt.hist(y)
plt.xlabel("Label")
plt.ylabel("Count")
plt.show()

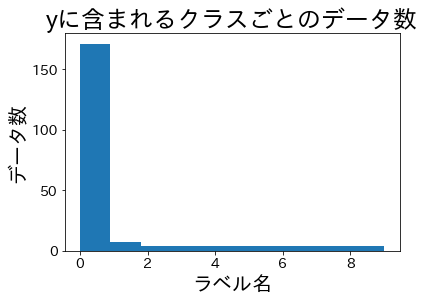
Experimental dataset figure

Class ratios after splitting #

Let’s split the data and verify the class proportions in the training and validation folds.

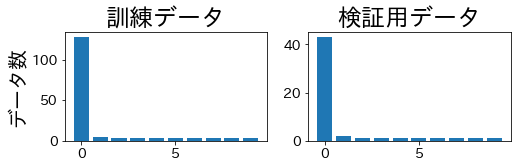
StratifiedKFold #

The class balance is maintained across both training and validation folds.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
skf = StratifiedKFold(n_splits=4)
for train_index, valid_index in skf.split(X, y):
    X_train, X_valid = X[train_index], X[valid_index]
    y_train, y_valid = y[train_index], y[valid_index]
    plt.figure(figsize=(8, 2))
    plt.subplot(121)
    plt.title("Training data")
    train_label_cnt = [(y_train == i).sum() for i in range(n_classes)]
    plt.ylabel("Count")
    plt.bar(np.arange(n_classes), train_label_cnt)
    plt.subplot(122)
    plt.title("Validation data")
    valid_label_cnt = [(y_valid == i).sum() for i in range(n_classes)]
    plt.bar(np.arange(n_classes), valid_label_cnt)
    plt.show()

The class balance is maintained across both training and val… figure

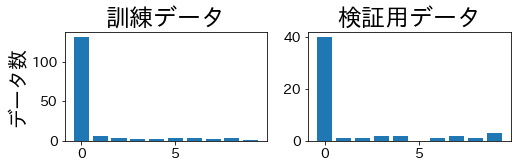
KFold #

Standard k-fold can produce validation folds that completely miss some minority classes.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
kf = KFold(n_splits=4)
for train_index, valid_index in kf.split(X, y):
    X_train, X_valid = X[train_index], X[valid_index]
    y_train, y_valid = y[train_index], y[valid_index]
    plt.figure(figsize=(8, 2))
    plt.subplot(121)
    plt.title("Training data")
    train_label_cnt = [(y_train == i).sum() for i in range(n_classes)]
    plt.ylabel("Count")
    plt.bar(np.arange(n_classes), train_label_cnt)
    plt.subplot(122)
    plt.title("Validation data")
    valid_label_cnt = [(y_valid == i).sum() for i in range(n_classes)]
    plt.bar(np.arange(n_classes), valid_label_cnt)
    plt.show()

Standard k-fold can produce validation folds that completely… figure

Practical considerations #

Extreme imbalance: when minority classes have only a handful of samples, consider combining stratification with repeated cross-validation to reduce variance further.
Regression tasks: use StratifiedKFold on discretised targets (binning) when cross-validation needs balanced target ranges.
Shuffle policy: set shuffle=True (with a fixed random seed) when the dataset has temporal or grouped ordering that might bias folds.

Stratified k-fold is a drop-in replacement for standard k-fold when class balance matters. It produces fairer validation splits, stabilises metrics such as ROC-AUC, and improves comparability among models trained on imbalanced datasets.