まとめ
- Validation curves visualise how training and validation scores change when a single hyperparameter varies.
- Use
validation_curveto sweep a regularisation coefficient, plot both curves, and spot the sweet spot. - Learn how to interpret the graph when tuning hyperparameters and what caveats to keep in mind.
1. What is a validation curve? #
A validation curve plots a given hyperparameter on the x-axis and both training/validation scores on the y-axis. Typical interpretation:
- Training high, validation low → the model is overfitting; increase regularisation or decrease model capacity.
- Both scores low → underfitting; relax regularisation or choose a more expressive model.
- Both scores high and close → near an optimal setting; confirm with additional metrics.
While a learning curve analyses “sample size vs. score”, a validation curve analyses “hyperparameter vs. score”.
2. Python example (SVC with C)
#
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import validation_curve
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
def plot_validation_curve_for_svc() -> None:
"""Plot and save the validation curve for the regularisation parameter of SVC."""
features, labels = make_classification(
n_samples=1200,
n_features=20,
n_informative=5,
n_redundant=2,
n_repeated=0,
n_classes=2,
weights=[0.6, 0.4],
flip_y=0.02,
class_sep=1.2,
random_state=42,
)
model = make_pipeline(StandardScaler(), SVC(kernel="rbf", gamma="scale"))
param_range = np.logspace(-3, 2, 10)
train_scores, valid_scores = validation_curve(
estimator=model,
X=features,
y=labels,
param_name="svc__C",
param_range=param_range,
scoring="roc_auc",
cv=5,
n_jobs=None,
)
train_mean = train_scores.mean(axis=1)
train_std = train_scores.std(axis=1)
valid_mean = valid_scores.mean(axis=1)
valid_std = valid_scores.std(axis=1)
plt.figure(figsize=(7, 5))
plt.semilogx(param_range, train_mean, label="Train score", color="#1d4ed8")
plt.fill_between(
param_range,
train_mean - train_std,
train_mean + train_std,
alpha=0.2,
color="#1d4ed8",
)
plt.semilogx(param_range, valid_mean, label="Validation score", color="#ea580c")
plt.fill_between(
param_range,
valid_mean - valid_std,
valid_mean + valid_std,
alpha=0.2,
color="#ea580c",
)
plt.title("Validation Curve for SVC (ROC-AUC)")
plt.xlabel("Regularisation parameter C")
plt.ylabel("Score")
plt.ylim(0.5, 1.05)
plt.legend(loc="best")
plt.grid(alpha=0.3)
plot_validation_curve_for_svc()
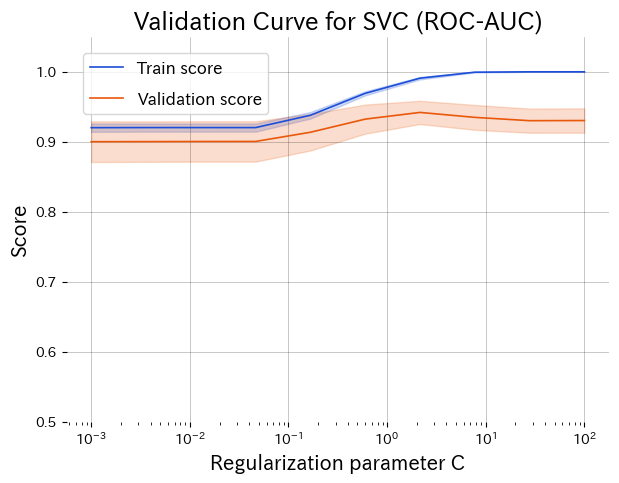
Lower C over-regularises, higher C overfits. The peak around C ≈ 1 gives the best validation score.
3. Reading the graph #
- Left side (small C): strong regularisation causes underfitting; both scores are low.
- Right side (large C): weak regularisation leads to high training score but falling validation score (overfitting).
- Middle peak: training and validation curves converge, indicating a good trade-off.
4. Applying it in practice #
- Pre-tune exploration: identify a promising hyperparameter range before running expensive searches (grid, random, Bayesian).
- Check variance: look at the shaded error bands (standard deviation) to judge stability, especially with small datasets.
- Prioritise multiple parameters: create validation curves for key parameters to decide which ones deserve deeper search.
- Combine with learning curves: understand “what hyperparameter works” and “whether more data helps” simultaneously.
Validation curves make the direction of hyperparameter tuning intuitive and support decision-making across the team. Keeping these plots for each production model streamlines discussions about next steps.