Correlation coefficient

Correlation coefficient measures the strength of a linear relationship between two data or random variables.

It is an indicator that allows us to check whether there is a trend change of linear form between two variables, which can be expressed in the following equation.

$

\frac{\Sigma_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma_{i=1}^N(x_i - \bar{x})^2 \Sigma_{i=1}^N(y_i - \bar{y})^2 }}

$

It has the following properties

• • 1 to less than 1

• If correlation coefficient is close to 1, \(x\) increases → \(y\) also increases

• The value of correlation coefficient does not change when \(x, y\) are multiplied by a low number

Calculate the correlation coefficient between two numerical columns #

1
2
3

import numpy as np

np.random.seed(777)  # to fix random numbers

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

import matplotlib.pyplot as plt

import numpy as np

x = [xi + np.random.rand() for xi in np.linspace(0, 100, 40)]

y = [yi + np.random.rand() for yi in np.linspace(1, 50, 40)]

plt.figure(figsize=(5, 5))

plt.scatter(x, y)

plt.show()

coef = np.corrcoef(x, y)

print(coef)

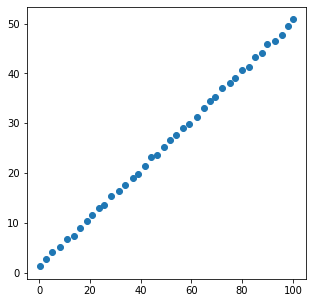
[[1.         0.99979848]

 [0.99979848 1.        ]]

Collectively compute the correlation coefficient between multiple variables #

1
2
3
4
5

import seaborn as sns

df = sns.load_dataset("iris")

df.head()

<tr style="text-align: right;">

  <th></th>

  <th>sepal_length</th>

  <th>sepal_width</th>

  <th>petal_length</th>

  <th>petal_width</th>

  <th>species</th>

</tr>

<tr>

  <th>0</th>

  <td>5.1</td>

  <td>3.5</td>

  <td>1.4</td>

  <td>0.2</td>

  <td>setosa</td>

</tr>

<tr>

  <th>1</th>

  <td>4.9</td>

  <td>3.0</td>

  <td>1.4</td>

  <td>0.2</td>

  <td>setosa</td>

</tr>

<tr>

  <th>2</th>

  <td>4.7</td>

  <td>3.2</td>

  <td>1.3</td>

  <td>0.2</td>

  <td>setosa</td>

</tr>

<tr>

  <th>3</th>

  <td>4.6</td>

  <td>3.1</td>

  <td>1.5</td>

  <td>0.2</td>

  <td>setosa</td>

</tr>

<tr>

  <th>4</th>

  <td>5.0</td>

  <td>3.6</td>

  <td>1.4</td>

  <td>0.2</td>

  <td>setosa</td>

</tr>

Check the CORRELATION COEFFICIENCES between all variables #

Using the iris dataset, let’s look at the correlation between variables.

1

df.corr().style.background_gradient(cmap="YlOrRd")

<tr>

  <th class="blank level0" >&nbsp;</th>

  <th class="col_heading level0 col0" >sepal_length</th>

  <th class="col_heading level0 col1" >sepal_width</th>

  <th class="col_heading level0 col2" >petal_length</th>

  <th class="col_heading level0 col3" >petal_width</th>

</tr>

<tr>

  <th id="T_dbd76_level0_row0" class="row_heading level0 row0" >sepal_length</th>

  <td id="T_dbd76_row0_col0" class="data row0 col0" >1.000000</td>

  <td id="T_dbd76_row0_col1" class="data row0 col1" >-0.117570</td>

  <td id="T_dbd76_row0_col2" class="data row0 col2" >0.871754</td>

  <td id="T_dbd76_row0_col3" class="data row0 col3" >0.817941</td>

</tr>

<tr>

  <th id="T_dbd76_level0_row1" class="row_heading level0 row1" >sepal_width</th>

  <td id="T_dbd76_row1_col0" class="data row1 col0" >-0.117570</td>

  <td id="T_dbd76_row1_col1" class="data row1 col1" >1.000000</td>

  <td id="T_dbd76_row1_col2" class="data row1 col2" >-0.428440</td>

  <td id="T_dbd76_row1_col3" class="data row1 col3" >-0.366126</td>

</tr>

<tr>

  <th id="T_dbd76_level0_row2" class="row_heading level0 row2" >petal_length</th>

  <td id="T_dbd76_row2_col0" class="data row2 col0" >0.871754</td>

  <td id="T_dbd76_row2_col1" class="data row2 col1" >-0.428440</td>

  <td id="T_dbd76_row2_col2" class="data row2 col2" >1.000000</td>

  <td id="T_dbd76_row2_col3" class="data row2 col3" >0.962865</td>

</tr>

<tr>

  <th id="T_dbd76_level0_row3" class="row_heading level0 row3" >petal_width</th>

  <td id="T_dbd76_row3_col0" class="data row3 col0" >0.817941</td>

  <td id="T_dbd76_row3_col1" class="data row3 col1" >-0.366126</td>

  <td id="T_dbd76_row3_col2" class="data row3 col2" >0.962865</td>

  <td id="T_dbd76_row3_col3" class="data row3 col3" >1.000000</td>

</tr>

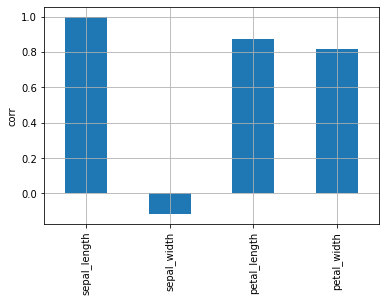
In the heatmap, it is hard to see where the correlation is highest. Check the bar chart to see which variables have the highest correlation with sepal_length.

1

df.corr()["sepal_length"].plot.bar(grid=True, ylabel="corr")

When correlation coefficient is low #

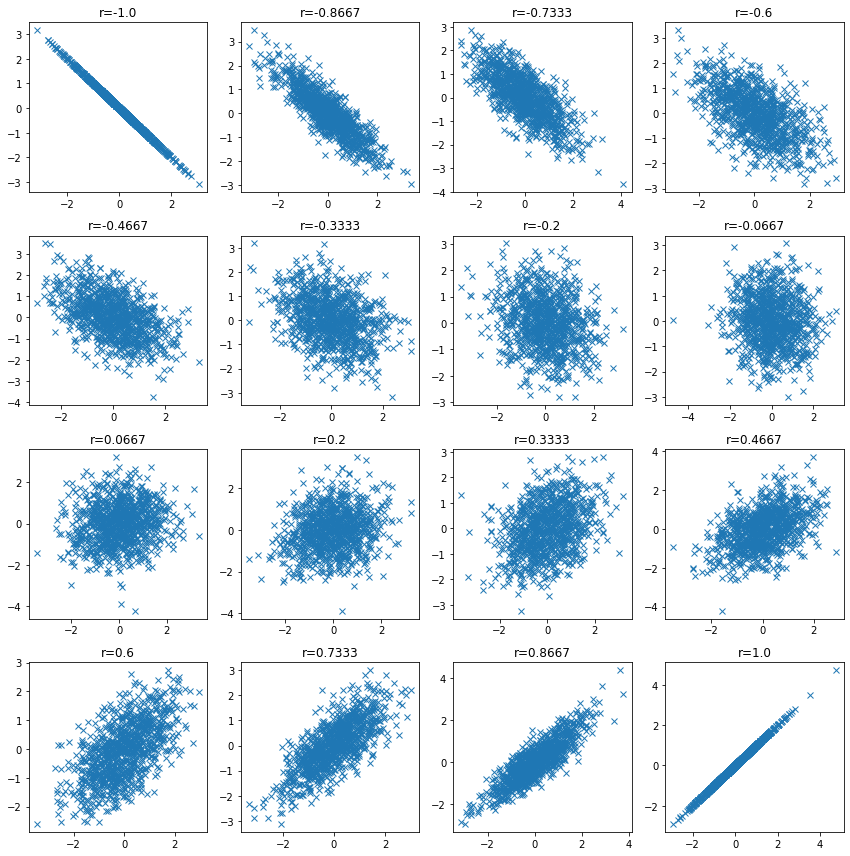
Check the data distribution when the correlation coefficient is low and confirm that the correlation coefficient may be low even when there is a relationship between variables.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

n_samples = 1000

plt.figure(figsize=(12, 12))

for i, ci in enumerate(np.linspace(-1, 1, 16)):

    ci = np.round(ci, 4)

    mean = np.array([0, 0])

    cov = np.array([[1, ci], [ci, 1]])

    v1, v2 = np.random.multivariate_normal(mean, cov, size=n_samples).T

    plt.subplot(4, 4, i + 1)

    plt.plot(v1, v2, "x")

    plt.title(f"r={ci}")

plt.tight_layout()

plt.show()

In some cases, there is a relationship between variables even if the correlation coefficient is low.

We will try to create such an example, albeit a simple one.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

import japanize_matplotlib

from sklearn import datasets

japanize_matplotlib.japanize()

n_samples = 1000

circle, _ = datasets.make_circles(n_samples=n_samples, factor=0.1, noise=0.05)

moon, _ = datasets.make_moons(n_samples=n_samples, noise=0.05)

corr_circle = np.round(np.corrcoef(circle[:, 0], circle[:, 1])[1, 0], 4)

plt.title(f"correlation coefficient={corr_circle}", fontsize=23)

plt.scatter(circle[:, 0], circle[:, 1])

plt.show()

corr_moon = np.round(np.corrcoef(moon[:, 0], moon[:, 1])[1, 0], 4)

plt.title(f"correlation coefficient={corr_moon}", fontsize=23)

plt.scatter(moon[:, 0], moon[:, 1])

plt.show()