Correlation coefficient
Correlation coefficient measures the strength of a linear relationship between two data or random variables. It is an indicator that allows us to check whether there is a trend change of linear form between two variables, which can be expressed in the following equation.
$ \frac{\Sigma_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma_{i=1}^N(x_i - \bar{x})^2 \Sigma_{i=1}^N(y_i - \bar{y})^2 }} $
It has the following properties
- 1 to less than 1
- If correlation coefficient is close to 1, $x$ increases → $y$ also increases
- The value of correlation coefficient does not change when $x, y$ are multiplied by a low number
Calculate the correlation coefficient between two numerical columns
import numpy as np
np.random.seed(777) # to fix random numbers
import matplotlib.pyplot as plt
import numpy as np
x = [xi + np.random.rand() for xi in np.linspace(0, 100, 40)]
y = [yi + np.random.rand() for yi in np.linspace(1, 50, 40)]
plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.show()
coef = np.corrcoef(x, y)
print(coef)
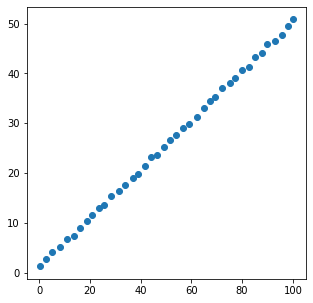
[[1. 0.99979848]
[0.99979848 1. ]]
Collectively compute the correlation coefficient between multiple variables
import seaborn as sns
df = sns.load_dataset("iris")
df.head()
| sepal_length | sepal_width | petal_length | petal_width | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
Check the CORRELATION COEFFICIENCES between all variables
Using the iris dataset, let’s look at the correlation between variables.
df.corr().style.background_gradient(cmap="YlOrRd")
| sepal_length | sepal_width | petal_length | petal_width | |
|---|---|---|---|---|
| sepal_length | 1.000000 | -0.117570 | 0.871754 | 0.817941 |
| sepal_width | -0.117570 | 1.000000 | -0.428440 | -0.366126 |
| petal_length | 0.871754 | -0.428440 | 1.000000 | 0.962865 |
| petal_width | 0.817941 | -0.366126 | 0.962865 | 1.000000 |
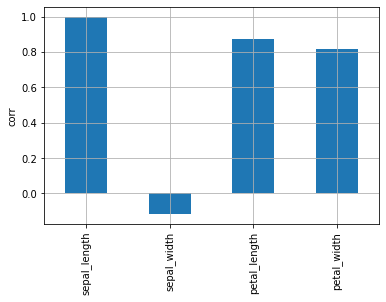
In the heatmap, it is hard to see where the correlation is highest. Check the bar chart to see which variables have the highest correlation with sepal_length.
df.corr()["sepal_length"].plot.bar(grid=True, ylabel="corr")
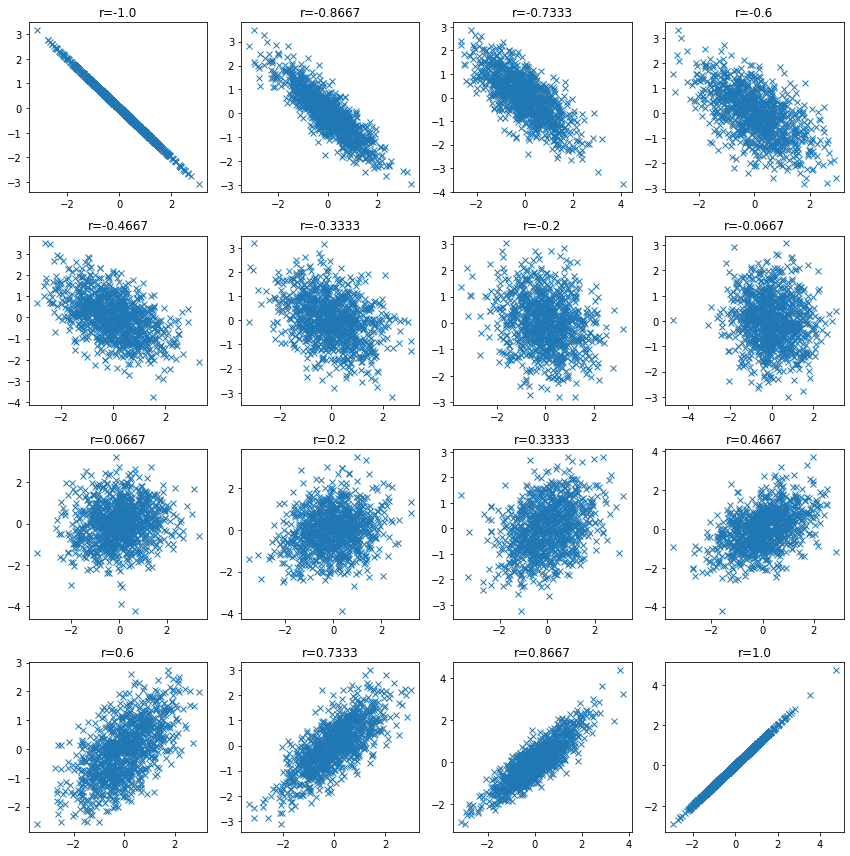
When correlation coefficient is low
Check the data distribution when the correlation coefficient is low and confirm that the correlation coefficient may be low even when there is a relationship between variables.
n_samples = 1000
plt.figure(figsize=(12, 12))
for i, ci in enumerate(np.linspace(-1, 1, 16)):
ci = np.round(ci, 4)
mean = np.array([0, 0])
cov = np.array([[1, ci], [ci, 1]])
v1, v2 = np.random.multivariate_normal(mean, cov, size=n_samples).T
plt.subplot(4, 4, i + 1)
plt.plot(v1, v2, "x")
plt.title(f"r={ci}")
plt.tight_layout()
plt.show()
In some cases, there is a relationship between variables even if the correlation coefficient is low. We will try to create such an example, albeit a simple one.
import japanize_matplotlib
from sklearn import datasets
japanize_matplotlib.japanize()
n_samples = 1000
circle, _ = datasets.make_circles(n_samples=n_samples, factor=0.1, noise=0.05)
moon, _ = datasets.make_moons(n_samples=n_samples, noise=0.05)
corr_circle = np.round(np.corrcoef(circle[:, 0], circle[:, 1])[1, 0], 4)
plt.title(f"correlation coefficient={corr_circle}", fontsize=23)
plt.scatter(circle[:, 0], circle[:, 1])
plt.show()
corr_moon = np.round(np.corrcoef(moon[:, 0], moon[:, 1])[1, 0], 4)
plt.title(f"correlation coefficient={corr_moon}", fontsize=23)
plt.scatter(moon[:, 0], moon[:, 1])
plt.show()

