Coefficient of determination

Last updated 2020-02-12 Read time 4 min

Summary

Understand the fundamentals of this metric, what it evaluates, and how to interpret the results.
Compute and visualise the metric with Python 3.13 code examples, covering key steps and practical checkpoints.
Combine charts and complementary metrics for effective model comparison and threshold tuning.

The coefficient of determination is a value in statistics that expresses how much of the dependent variable (objective variable) is explained by the independent variable (explanatory variable).

Generally, the higher the better the rating indicator
The best case is 1.
However, the more features you add, the higher the score tends to be.
Therefore, it is not possible to judge “high accuracy of the model” by looking at this indicator alone

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np

import matplotlib.pyplot as plt

import japanize_matplotlib

from sklearn.datasets import make_regression

from sklearn.ensemble import RandomForestRegressor

from sklearn.model_selection import train_test_split

python

Create models and calculate coefficients of determination for sample data #

First, let’s create data that makes predictions more likely to be correct.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

python

Calculate coefficient of determination #

sklearn.metrics.roc_auc_score

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
from sklearn.metrics import r2_score

r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("target")

plt.ylabel("prediction")

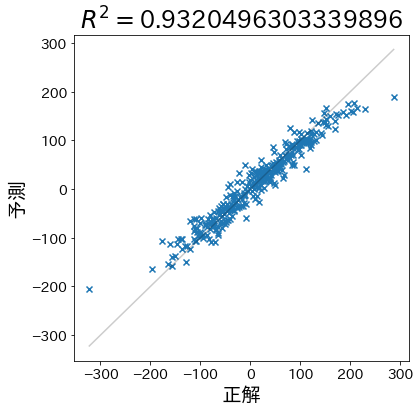
Calculate coefficient of determination figure

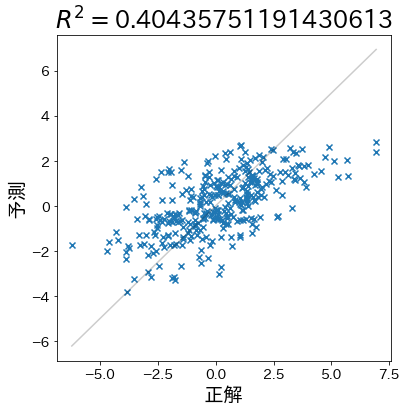
Next, create data for which the predictions are less likely to be correct and check to see that the coefficient of determination falls.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("target")

plt.ylabel("prediction")

Next, create data for which the predictions are less likely… figure

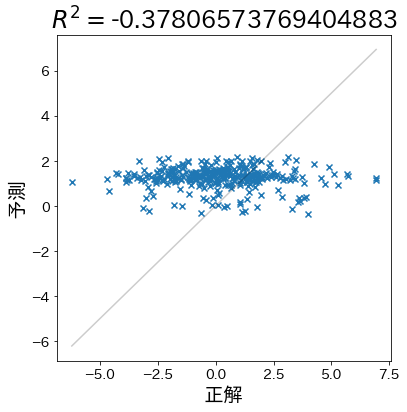
When the prediction is almost random #

When the accuracy is even worse than simply predicting the average, the coefficient of determination is negative.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

# Randomly reorder train_y and convert values

train_y = np.random.permutation(train_y)

train_y = np.sin(train_y) * 10 + 1

model = RandomForestRegressor(max_depth=1)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("target")

plt.ylabel("prediction")

When the accuracy is even worse than simply predicting the a… figure

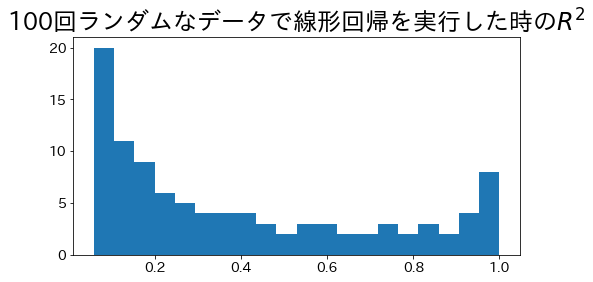
Coefficient of determination when using the least squares method #

In the case of a regression line for a single regression using the least squares method, the range of the coefficient of determination is \( 0 \le R^2 \le 1\).

Let us try to find the coefficient of determination by running a 100-line regression with random noise on the data.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
from sklearn.linear_model import LinearRegression

from sklearn.pipeline import make_pipeline

from sklearn.preprocessing import StandardScaler

r2_scores = []

for i in range(100):

    X, y = make_regression(

        n_samples=500,

        n_informative=1,

        n_features=1,

        effective_rank=4,

        noise=i * 0.1,

        random_state=RND,

    )

    train_X, test_X, train_y, test_y = train_test_split(

        X, y, test_size=0.33, random_state=RND

    )

    # linear regression

    model = make_pipeline(

        StandardScaler(with_mean=False), LinearRegression(positive=True)

    ).fit(train_X, train_y)

    # Calculate coefficient of determination

    pred_y = model.predict(test_X)

    r2 = r2_score(test_y, pred_y)

    r2_scores.append(r2)

plt.figure(figsize=(8, 4))

plt.hist(r2_scores, bins=20)

plt.show()

Let us try to find the coefficient of determination by runni… figure