Coefficient of determination
The coefficient of determination is a value in statistics that expresses how much of the dependent variable (objective variable) is explained by the independent variable (explanatory variable).
- Generally, the higher the better the rating indicator
- The best case is 1.
- However, the more features you add, the higher the score tends to be.
- Therefore, it is not possible to judge “high accuracy of the model” by looking at this indicator alone
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
Create models and calculate coefficients of determination for sample data
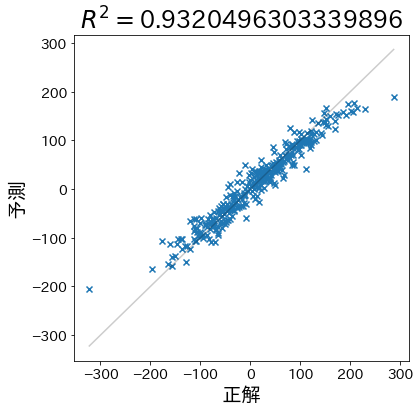
First, let’s create data that makes predictions more likely to be correct.
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
model = RandomForestRegressor(max_depth=5)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
Calculate coefficient of determination
from sklearn.metrics import r2_score
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("target")
plt.ylabel("prediction")
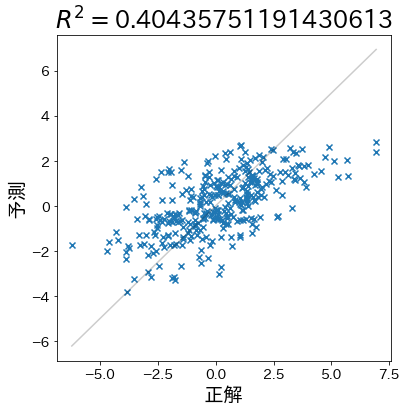
Next, create data for which the predictions are less likely to be correct and check to see that the coefficient of determination falls.
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
effective_rank=4,
noise=1.5,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
model = RandomForestRegressor(max_depth=5)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("target")
plt.ylabel("prediction")
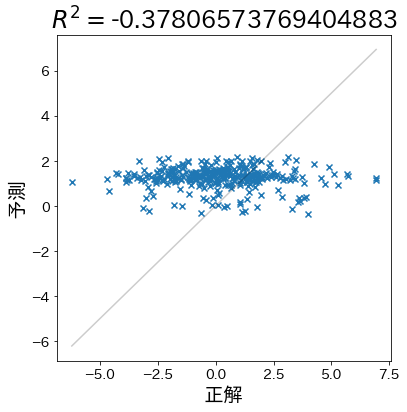
When the prediction is almost random
When the accuracy is even worse than simply predicting the average, the coefficient of determination is negative.
X, y = make_regression(
n_samples=1000,
n_informative=3,
n_features=20,
effective_rank=4,
noise=1.5,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
# Randomly reorder train_y and convert values
train_y = np.random.permutation(train_y)
train_y = np.sin(train_y) * 10 + 1
model = RandomForestRegressor(max_depth=1)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)
plt.figure(figsize=(6, 6))
plt.title(f"$R^2 =${r2}")
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("target")
plt.ylabel("prediction")
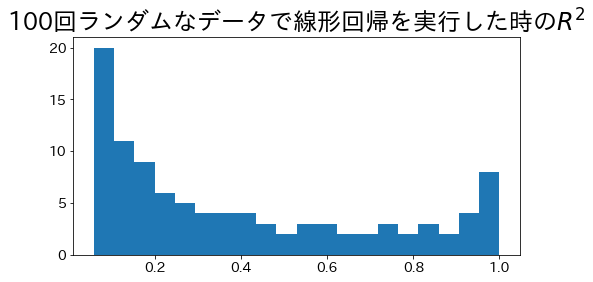
Coefficient of determination when using the least squares method
In the case of a regression line for a single regression using the least squares method, the range of the coefficient of determination is $ 0 \le R^2 \le 1$. Let us try to find the coefficient of determination by running a 100-line regression with random noise on the data.
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
r2_scores = []
for i in range(100):
X, y = make_regression(
n_samples=500,
n_informative=1,
n_features=1,
effective_rank=4,
noise=i * 0.1,
random_state=RND,
)
train_X, test_X, train_y, test_y = train_test_split(
X, y, test_size=0.33, random_state=RND
)
# linear regression
model = make_pipeline(
StandardScaler(with_mean=False), LinearRegression(positive=True)
).fit(train_X, train_y)
# Calculate coefficient of determination
pred_y = model.predict(test_X)
r2 = r2_score(test_y, pred_y)
r2_scores.append(r2)
plt.figure(figsize=(8, 4))
plt.hist(r2_scores, bins=20)
plt.show()