AR Process

Last updated 2020-03-25 Read time 2 min

AR models are also known as autoregressive models. As the name autoregressive implies, it refers to a stochastic process in which the output of the model at time t depends on its own output before time t.

1
2
3
import statsmodels.api as sm
import numpy as np
import matplotlib.pyplot as plt

Create data for AR process #

Prepare functions to generate data

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
def create_ARdata(phis=[0.1], N=500, init=1, c=1, sigma=0.3):
    """Generating AR process data"""
    print(f"==AR({len(phis)}), #data={N}==")
    data = np.zeros(N)
    data[0] = init + np.random.normal(0, sigma)

    for t in range(2, N):
        res = c + np.random.normal(0, sigma)
        for j, phi_j in enumerate(phis):
            res += phi_j * data[t - j - 1]
        data[t] = res
    return data

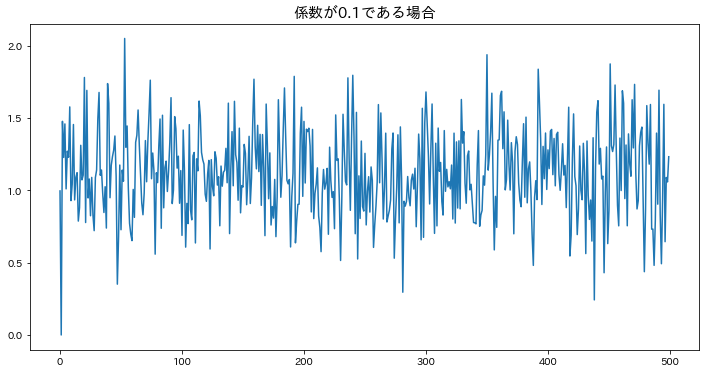
φ < 1 #

1
2
3
4
5
plt.figure(figsize=(12, 6))
phis = [0.1]
ar1_1 = create_ARdata(phis=phis)
plt.plot(ar1_1)
plt.show()

==AR(1), #data=500==

==AR(1), #data=500== figure

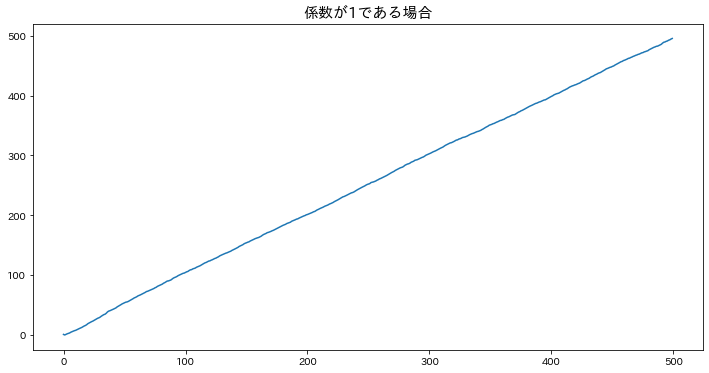
φ = 1 #

1
2
3
4
5
plt.figure(figsize=(12, 6))
phis = [1]
ar1_2 = create_ARdata(phis=phis)
plt.plot(ar1_2)
plt.show()

==AR(1), #data=500==

==AR(1), #data=500== figure

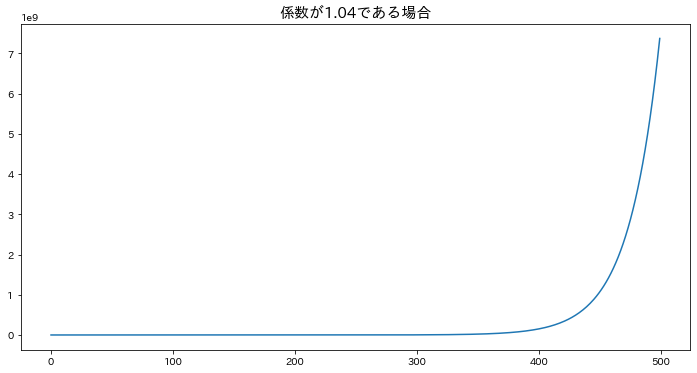
φ > 1 #

1
2
3
4
5
plt.figure(figsize=(12, 6))
phis = [1.04]
ar1_2 = create_ARdata(phis=phis)
plt.plot(ar1_2)
plt.show()

==AR(1), #data=500==

==AR(1), #data=500== figure

AR(2) #

1
2
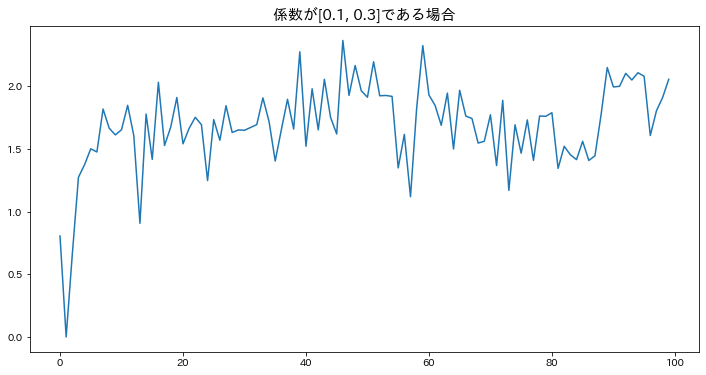
3
4
5
plt.figure(figsize=(12, 6))
phis = [0.1, 0.3]
ar2_1 = create_ARdata(phis=phis, N=100)
plt.plot(ar2_1)
plt.show()

==AR(2), #data=100==

==AR(2), #data=100== figure

1
2
3
4
5
plt.figure(figsize=(12, 6))
phis = [0.1, -1.11]
ar2_1 = create_ARdata(phis=phis)
plt.plot(ar2_1)
plt.show()

==AR(2), #data=500==

==AR(2), #data=500== figure

Estimate the autoregressive (AR) model #

1
2
3
4
5
6
from statsmodels.tsa.ar_model import AutoReg

res = AutoReg(ar1_1, lags=1).fit()

out = "AIC: {0:0.3f}, HQIC: {1:0.3f}, BIC: {2:0.3f}"
print(out.format(res.aic, res.hqic, res.bic))

AIC: 231.486, HQIC: 236.445, BIC: 244.124

1
2
3
print(res.params)
print(res.sigma2)
res.summary()

[1.03832755 0.07236388]
0.09199676371696269

AutoReg Model Results
Dep. Variable:	y	No. Observations:	500
Model:	AutoReg(1)	Log Likelihood	-112.743
Method:	Conditional MLE	S.D. of innovations	0.303
Date:	Sat, 13 Aug 2022	AIC	231.486
Time:	01:55:17	BIC	244.124
Sample:	1	HQIC	236.445
	500

	coef	std err	z	P>\|z\|	[0.025	0.975]
const	1.0383	0.052	20.059	0.000	0.937	1.140
y.L1	0.0724	0.045	1.621	0.105	-0.015	0.160

Roots
	Real	Imaginary	Modulus	Frequency
AR.1	13.8190	+0.0000j	13.8190	0.0000

MA Process — Stochastic process expressing current value as a linear combination of errors