Check Dataset

入門

5.10.1

Check Dataset

Last updated 2020-01-29 Read time 3 min

See what’s in the data #

1
2
3
4
5
6
7
8

import datetime
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

from scipy import stats
from statsmodels.tsa import stattools

Reading a dataset from a csv file #

1
2

data = pd.read_csv("sample.csv")
data.head(10)

DateTemp
01981-01-0120.7
11981-01-0217.9
21981-01-0318.8
31981-01-0414.6
41981-01-0515.8
51981-01-0615.8
61981-01-0715.8
71981-01-0817.4
81981-01-0921.8
91981-01-1020.0

Set timestamp to datetime #

The Date column is currently read as an Object type, i.e., a string. To treat it as a timestamp, use the following datetime — Basic Date and Time Types to convert it to a datetime type.

1
2
3
4
5

data["Date"] = data["Date"].apply(
    lambda x: datetime.datetime.strptime(str(x), "%Y-%m-%d")
)

print(f"Date column dtype: {data['Date'].dtype}")

Date column dtype: datetime64[ns]

Get an overview of a time series #

pandas.DataFrame.describe #

To begin, we briefly review what the data looks like. We will use pandas.DataFrame.describe to check some simple statistics for the Temp column.

1

data.describe()

Temp
count3650.000000
mean11.177753
std4.071837
min0.000000
25%8.300000
50%11.000000
75%14.000000
max26.300000

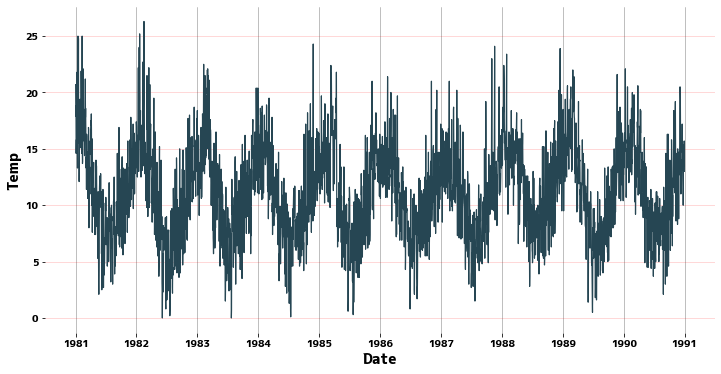
Line graph #

Use seaborn.lineplot to see what the cycle looks like.

1
2
3
4
5
6

plt.figure(figsize=(12, 6))
sns.lineplot(x=data["Date"], y=data["Temp"])
plt.ylabel("Temp")
plt.grid(axis="x")
plt.grid(axis="y", color="r", alpha=0.3)
plt.show()

lineplot to see what the cycle looks like figure

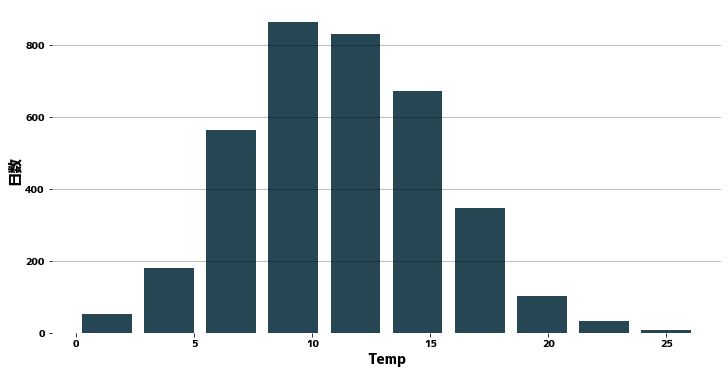
Histogram #

1
2
3
4
5
6

plt.figure(figsize=(12, 6))
plt.hist(x=data["Temp"], rwidth=0.8)
plt.xlabel("Temp")
plt.ylabel("日数")
plt.grid(axis="y")
plt.show()

Histogram figure

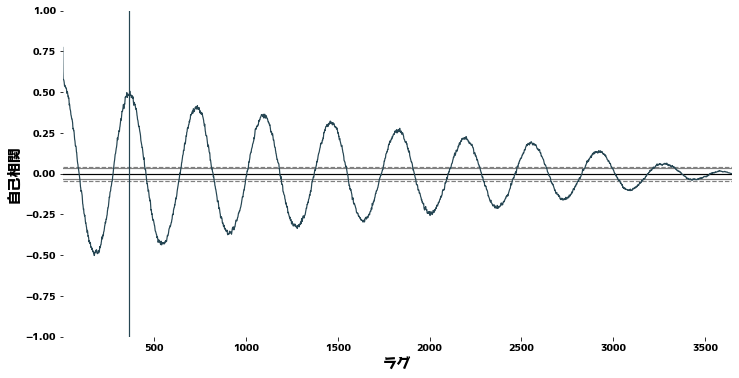
Autocorrelation and Cholerograms #

Using pandas.plotting.autocorrelation_plot Check autocorrelation to check the periodicity of time series data. Roughly speaking, autocorrelation is a measure of how well a signal matches a time-shifted signal of itself, expressed as a function of the magnitude of the time shift.

1
2
3
4
5
6
7

plt.figure(figsize=(12, 6))
pd.plotting.autocorrelation_plot(data["Temp"])
plt.grid()
plt.axvline(x=365)
plt.xlabel("lag")
plt.ylabel("autocorrelation")
plt.show()

Roughly speaking, autocorrelation is a measure of how well a… figure

Unit Root Test #

We check to see if the data are a unit root process. The Augmented Dickey-Fuller test is used to test the null hypothesis of a unit root process.

statsmodels.tsa.stattools.adfuller

1

stattools.adfuller(data["Temp"], autolag="AIC")

(-4.444804924611697,
 0.00024708263003610177,
 20,
 3629,
 {'1%': -3.4321532327220154,
  '5%': -2.862336767636517,
  '10%': -2.56719413172842},
 16642.822304301197)

Checking the trend #

The trend line is drawn by fitting a one-dimensional polynomial to the time series. Since the data in this case is almost trend-stationary, there is almost no trend.

numpy.poly1d — NumPy v1.22 Manual

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def get_trend(timeseries, deg=3):
    """Create a trend line for time-series data

    Args:
        timeseries(pd.Series) : time-series data

    Returns:
        pd.Series: trend line
    """
    x = list(range(len(timeseries)))
    y = timeseries.values
    coef = np.polyfit(x, y, deg)
    trend = np.poly1d(coef)(x)
    return pd.Series(data=trend, index=timeseries.index)

data["Trend"] = get_trend(data["Temp"])

# グラフをプロット
plt.figure(figsize=(12, 6))
sns.lineplot(x=data["Date"], y=data["Temp"], alpha=0.5, label="Temp")
sns.lineplot(x=data["Date"], y=data["Trend"], label="トレンド")
plt.grid(axis="x")
plt.legend()
plt.show()

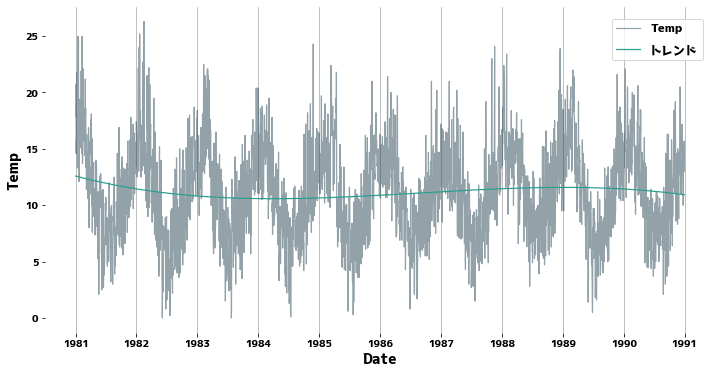
22 Manual figure

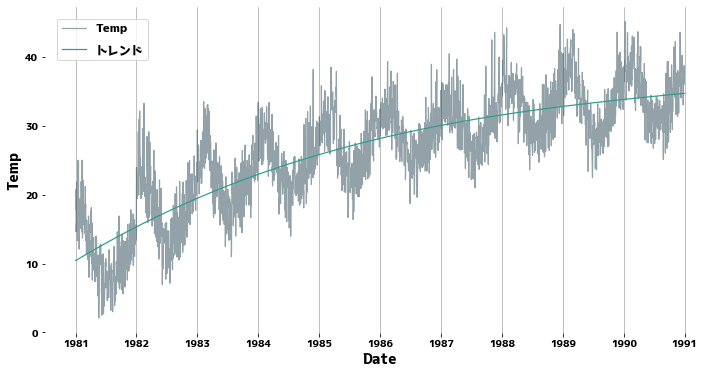
Supplement: If there is a clear trend #

The green line is the trend line.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

data_sub = data.copy()
data_sub["Temp"] = (
    data_sub["Temp"] + np.log(data_sub["Date"].dt.year - 1980) * 10
)  # Dummy Trends
data_sub["Trend"] = get_trend(data_sub["Temp"])

plt.figure(figsize=(12, 6))
sns.lineplot(x=data_sub["Date"], y=data_sub["Temp"], alpha=0.5, label="Temp")
sns.lineplot(x=data_sub["Date"], y=data_sub["Trend"], label="トレンド")
plt.grid(axis="x")
plt.legend()
plt.show()

The green line is the trend line figure