Dynamic Time Warping

Timeseries

Dynamic Time Warping

Created: Last updated: Read time: 3 min
まとめ
  • Dynamic Time Warping (DTW) aligns two time series while allowing for local stretching or shrinking of the time axis.
  • The algorithm builds a distance matrix, computes cumulative costs with dynamic programming, and retrieves the minimal warping path.
  • We implement DTW with NumPy, compare it with fastdtw, and visualise how the optimal alignment behaves.

What is DTW? #

DTW measures the similarity between two sequences that may vary in speed or starting phase. It aligns the sequences by finding the path with the minimum cumulative distance. Typical applications include speech recognition, activity recognition from sensors, and recommendation systems that compare temporal usage patterns.

DTW in NumPy #

import numpy as np

def dtw_distance(
    x: np.ndarray,
    y: np.ndarray,
    window: int | None = None,
) -> tuple[float, list[tuple[int, int]]]:
    n, m = len(x), len(y)
    window = max(window or max(n, m), abs(n - m))

    cost = np.full((n + 1, m + 1), np.inf)
    cost[0, 0] = 0.0

    for i in range(1, n + 1):
        for j in range(max(1, i - window), min(m + 1, i + window + 1)):
            dist = abs(x[i - 1] - y[j - 1])
            cost[i, j] = dist + min(cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1])

    i, j = n, m
    path: list[tuple[int, int]] = []
    while i > 0 and j > 0:
        path.append((i - 1, j - 1))
        idx = np.argmin((cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1]))
        if idx == 0:
            i -= 1
        elif idx == 1:
            j -= 1
        else:
            i -= 1
            j -= 1

    path.reverse()
    return cost[n, m], path

Comparing three series #

python --version  # e.g. Python 3.13.0
pip install matplotlib fastdtw

import matplotlib.pyplot as plt
from fastdtw import fastdtw

np.random.seed(42)
t = np.arange(0, 30)

series_a = 1.2 * np.sin(t / 2.0)
series_b = 1.1 * np.sin((t + 2) / 2.1) + 0.05 * np.random.randn(len(t))
series_c = 0.8 * np.cos(t / 2.0) + 0.05 * np.random.randn(len(t))

plt.figure(figsize=(10, 3))
plt.plot(t, series_a, label="Series A", color="black")
plt.plot(t, series_b, label="Series B", color="tab:red")
plt.plot(t, series_c, label="Series C", color="tab:blue")
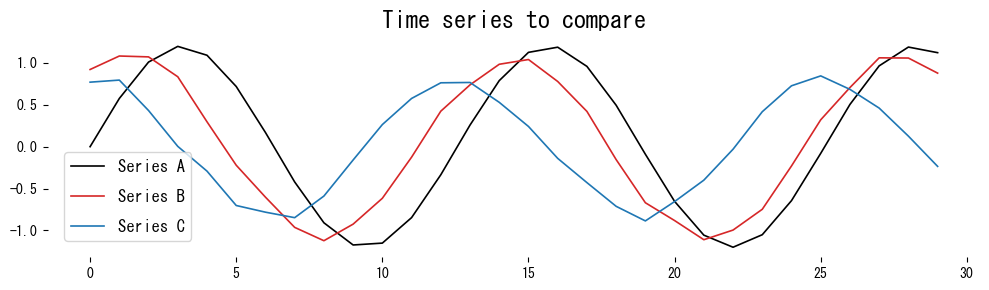
plt.title("Time series to compare")
plt.legend()
plt.tight_layout()
plt.show()

Comparing three series figure

dist_ab, path_ab = dtw_distance(series_a, series_b)
dist_ac, path_ac = dtw_distance(series_a, series_c)

fast_dist_ab, _ = fastdtw(series_a, series_b)
fast_dist_ac, _ = fastdtw(series_a, series_c)

print(f"DTW(A, B)  = {dist_ab:.3f}  / fastdtw = {fast_dist_ab:.3f}")
print(f"DTW(A, C)  = {dist_ac:.3f}  / fastdtw = {fast_dist_ac:.3f}")

Series B has a similar shape to Series A, so both DTW and fastdtw report a small distance. Series C differs in shape and therefore yields a larger distance.

Visualising the warping path #

def plot_warping(a: np.ndarray, b: np.ndarray, path: list[tuple[int, int]]) -> None:
    fig, axes = plt.subplots(
        1,
        2,
        figsize=(12, 4),
        gridspec_kw={"width_ratios": [1, 1.2]},
    )

    axes[0].plot(a, label="Series A", color="black")
    axes[0].plot(b, label="Series B", color="tab:red")
    axes[0].set_title("Time series")
    axes[0].legend()

    axes[1].imshow(
        np.abs(np.subtract.outer(a, b)),
        origin="lower",
        interpolation="nearest",
        cmap="viridis",
    )
    path_arr = np.array(path)
    axes[1].plot(path_arr[:, 1], path_arr[:, 0], color="white", linewidth=2)
    axes[1].set_title("Cumulative cost and warping path")
    axes[1].set_xlabel("Series B index")
    axes[1].set_ylabel("Series A index")
    plt.tight_layout()
    plt.show()

plot_warping(series_a, series_b, path_ab)

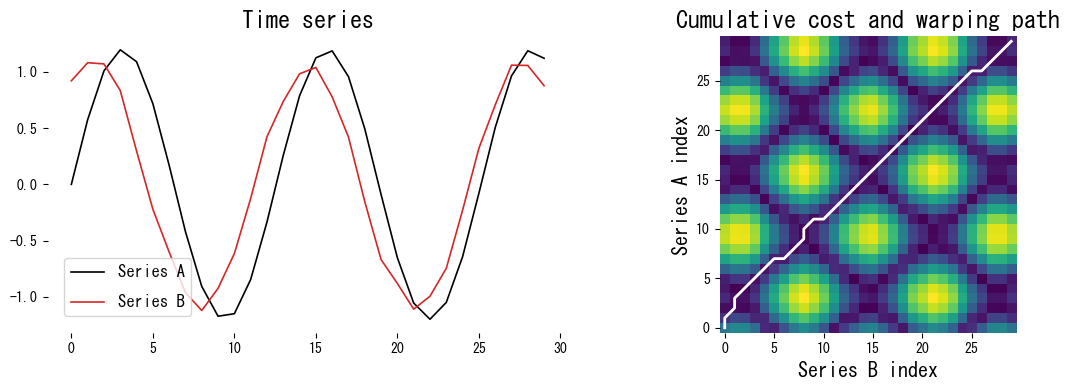
Visualising the warping path figure

The white path reveals how the algorithm stretches Series A and Series B so that peaks and valleys align even when they are shifted in time.

Takeaways #

  • DTW aligns sequences with varying tempo by minimising cumulative distance along a warping path.
  • Dynamic programming computes the optimal path; window constraints or fastdtw can speed things up.
  • NumPy is sufficient for a basic implementation, and the visualisation helps debug how DTW behaves on real data.