Dynamic Time Warping
DTW (Dynamic Time Warping) is one of the methods used to measure the similarity between time series data. When comparing two waveforms, it is not clear which point corresponds to which point if the lengths of the waveforms are different; DTW finds the distance between each point of two time series by brute force and finds the smallest combination among all patterns. In this way, it is possible to find waveforms that are "similar" in shape, even if the waves are slightly off. This page uses fastdtw to find the similarity between time series data.
import numpy as np
import matplotlib.pyplot as plt
from fastdtw import fastdtw
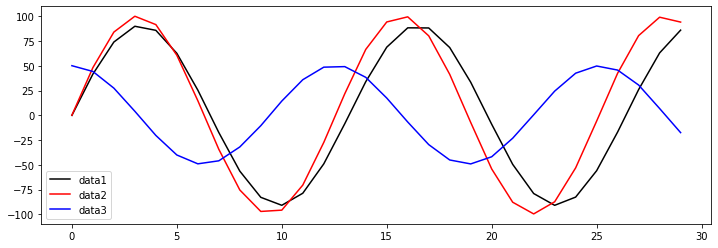
Plot the two waveforms used in the experiment
data1 = [91.0 * np.sin(i / 2.1) for i in range(30)]
data2 = [100.0 * np.sin(i / 2.0) + np.random.rand() for i in range(30)]
data3 = [50.0 * np.cos(i / 2.0) + np.random.rand() for i in range(30)]
plt.figure(figsize=(12, 4))
# Plotting Waveforms
plt.plot(data1, label="data1", color="k")
plt.plot(data2, label="data2", color="r")
plt.plot(data3, label="data3", color="b")
plt.legend()
plt.show()
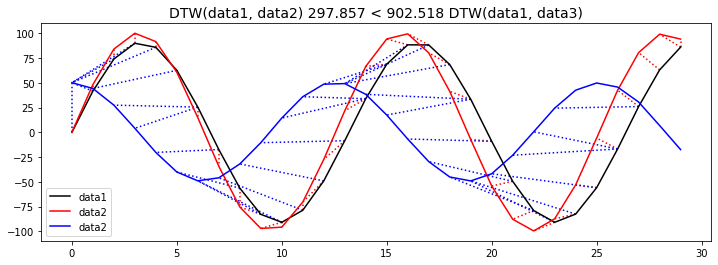
Calculate DTW and plot the correspondence
We can determine that the DTW between the black and red waveforms shows smaller DTW and is more similar (on the measure of DTW) than the blue waveform.
# Calculate DTW
distance_12, path_12 = fastdtw(data1, data2)
distance_13, path_13 = fastdtw(data1, data3)
# Connect corresponding points with a line
plt.figure(figsize=(12, 4))
for x_12, x_13 in zip(path_12, path_13):
plt.plot(x_12, [data1[x_12[0]], data2[x_12[1]]], color="r", linestyle="dotted")
plt.plot(x_13, [data1[x_13[0]], data3[x_13[1]]], color="b", linestyle="dotted")
# Plotting Waveforms
plt.plot(data1, label="data1", color="k")
plt.plot(data2, label="data2", color="r")
plt.plot(data3, label="data2", color="b")
plt.legend()
plt.title(
f"DTW(data1, data2) {np.round(distance_12, 3)} < {np.round(distance_13, 3)} DTW(data1, data3)",
fontsize=14,
)
plt.show()