Análisis discriminante lineal (LDA)

Actualizado 2020-03-11 Lectura 3 min

Resumen

LDA busca direcciones que maximizan la razón entre la varianza entre clases y la varianza intraclase, por lo que sirve tanto para clasificar como para reducir la dimensionalidad.
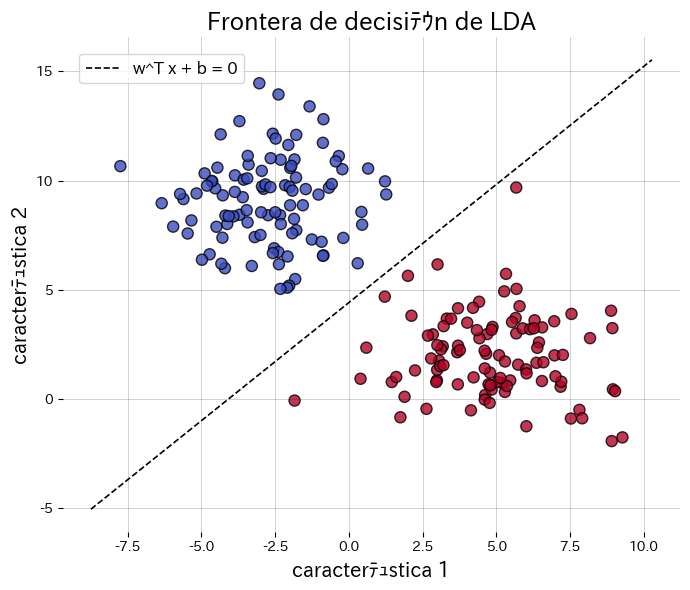
La frontera de decisión es de la forma $\mathbf{w}^\top \mathbf{x} + b = 0$; en 2D es una recta y en 3D un plano, lo que facilita su interpretación geométrica.
Si cada clase sigue una distribución gaussiana con igual matriz de covarianza, LDA se aproxima al clasificador bayesiano óptimo.
Con LinearDiscriminantAnalysis de scikit-learn es sencillo visualizar la frontera de decisión y examinar las características proyectadas.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

Para dos clases, la dirección de proyección $\mathbf{w}$ maximiza

$$ J(\mathbf{w}) = \frac{\mathbf{w}^\top \mathbf{S}_B \mathbf{w}}{\mathbf{w}^\top \mathbf{S}_W \mathbf{w}}, $$

donde $\mathbf{S}_B$ es la matriz de dispersión entre clases y $\mathbf{S}_W$ la matriz de dispersión intraclase. En el caso multiclase se obtienen hasta $K-1$ direcciones, útiles para reducir la dimensionalidad.

Experimentos con Python #

El código siguiente aplica LDA a un conjunto sintético de dos clases, dibuja la frontera de decisión y muestra la proyección a una dimensión. Con transform podemos obtener directamente los datos proyectados.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.metrics import accuracy_score

def run_lda_demo(
    n_samples: int = 200,
    random_state: int = 42,
    title_boundary: str = "Frontera de decisión de LDA",
    title_projection: str = "Proyección unidimensional con LDA",
    xlabel: str = "característica 1",
    ylabel: str = "característica 2",
    hist_xlabel: str = "característica proyectada",
    class0_label: str = "clase 0",
    class1_label: str = "clase 1",
) -> dict[str, float]:
    """Train LDA on synthetic blobs and plot boundary plus projection."""
    japanize_matplotlib.japanize()
    X, y = make_blobs(
        n_samples=n_samples,
        centers=2,
        n_features=2,
        cluster_std=2.0,
        random_state=random_state,
    )

    clf = LinearDiscriminantAnalysis(store_covariance=True)
    clf.fit(X, y)

    accuracy = float(accuracy_score(y, clf.predict(X)))
    w = clf.coef_[0]
    b = float(clf.intercept_[0])

    xs = np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 300)
    ys_boundary = -(w[0] / w[1]) * xs - b / w[1]

    fig, ax = plt.subplots(figsize=(7, 6))
    ax.set_title(title_boundary)
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k", alpha=0.8)
    ax.plot(xs, ys_boundary, "k--", lw=1.2, label="w^T x + b = 0")
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.legend(loc="best")
    ax.grid(alpha=0.25)
    fig.tight_layout()
    plt.show()

    X_proj = clf.transform(X)[:, 0]

    fig, ax = plt.subplots(figsize=(8, 4))
    ax.set_title(title_projection)
    ax.hist(X_proj[y == 0], bins=20, alpha=0.7, label=class0_label)
    ax.hist(X_proj[y == 1], bins=20, alpha=0.7, label=class1_label)
    ax.set_xlabel(hist_xlabel)
    ax.legend(loc="best")
    ax.grid(alpha=0.25)
    fig.tight_layout()
    plt.show()

    return {"accuracy": accuracy}

metrics = run_lda_demo(
    title_boundary="Frontera de decisión de LDA",
    title_projection="Proyección unidimensional con LDA",
    xlabel="característica 1",
    ylabel="característica 2",
    hist_xlabel="característica proyectada",
    class0_label="clase 0",
    class1_label="clase 1",
)
print(f"Precisión de entrenamiento: {metrics['accuracy']:.3f}")

Con transform podemos obtener directamente los datos proyect… (figura)

Referencias #

Fisher, R. A. (1936). The Use of Multiple Measurements in Taxonomic Problems. Annals of Eugenics, 7(2), 179"・88.
Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning. Springer.