Perceptrón

Actualizado 2020-02-26 Lectura 3 min

Resumen

El perceptrón converge en un número finito de actualizaciones si los datos son linealmente separables, siendo uno de los algoritmos de clasificación más antiguos.
La predicción se basa en el signo de $\mathbf{w}^\top \mathbf{x} + b$; cuando la señal es incorrecta, ese ejemplo actualiza los pesos.
La regla de actualización “敗umar el ejemplo mal clasificado escalado por la tasa de aprendizaje”・ofrece una introducción intuitiva a los métodos basados en gradiente.
Si los datos no son separables linealmente, conviene ampliar características o recurrir a kernel tricks.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

La predicción se calcula como

$$ \hat{y} = \operatorname{sign}(\mathbf{w}^\top \mathbf{x} + b). $$

Si un ejemplo $(\mathbf{x}_i, y_i)$ queda mal clasificado, se actualiza mediante

$$ \mathbf{w} \leftarrow \mathbf{w} + \eta\, y_i\, \mathbf{x}_i,\qquad b \leftarrow b + \eta\, y_i. $$

Cuando los datos son separables linealmente, este procedimiento converge.

Experimentos con Python #

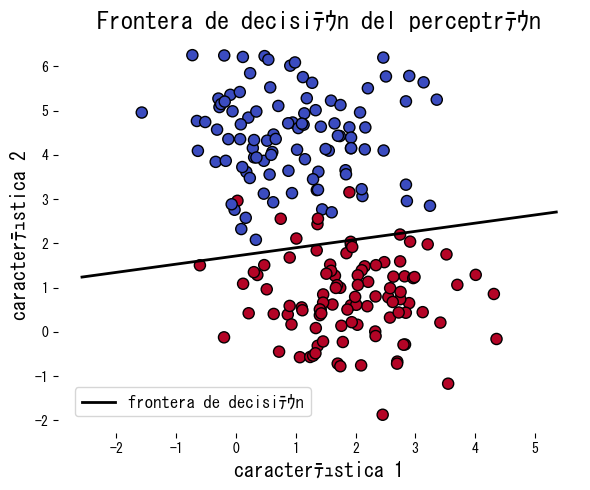
El siguiente ejemplo aplica el perceptrón a datos sintéticos, muestra el número de errores por época y dibuja la frontera obtenida.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
from sklearn.metrics import accuracy_score

def run_perceptron_demo(
    n_samples: int = 200,
    lr: float = 0.1,
    n_epochs: int = 20,
    random_state: int = 0,
    title: str = "Frontera de decisión del perceptrón",
    xlabel: str = "característica 1",
    ylabel: str = "característica 2",
    label_boundary: str = "frontera de decisión",
) -> dict[str, object]:
    """Train a perceptron on synthetic blobs and plot the decision boundary."""
    japanize_matplotlib.japanize()
    X, y = make_blobs(n_samples=n_samples, centers=2, cluster_std=1.0, random_state=random_state)
    y_signed = np.where(y == 0, -1, 1)

    w = np.zeros(X.shape[1])
    b = 0.0
    history: list[int] = []

    for _ in range(n_epochs):
        errors = 0
        for xi, target in zip(X, y_signed):
            update = lr * target if target * (np.dot(w, xi) + b) <= 0 else 0.0
            if update != 0.0:
                w += update * xi
                b += update
                errors += 1
        history.append(int(errors))
        if errors == 0:
            break

    preds = np.where(np.dot(X, w) + b >= 0, 1, -1)
    accuracy = float(accuracy_score(y_signed, preds))

    xx = np.linspace(X[:, 0].min() - 1, X[:, 0].max() + 1, 200)
    yy = -(w[0] * xx + b) / w[1]

    fig, ax = plt.subplots(figsize=(6, 5))
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k")
    ax.plot(xx, yy, color="black", linewidth=2, label=label_boundary)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    ax.set_title(title)
    ax.legend(loc="best")
    fig.tight_layout()
    plt.show()

    return {"weights": w, "bias": b, "errors": history, "accuracy": accuracy}

metrics = run_perceptron_demo(
    title="Frontera de decisión del perceptrón",
    xlabel="característica 1",
    ylabel="característica 2",
    label_boundary="frontera de decisión",
)
print(f"Precisión de entrenamiento: {metrics['accuracy']:.3f}")
print("Pesos:", metrics['weights'])
print(f"Sesgo: {metrics['bias']:.3f}")
print("Errores por época:", metrics['errors'])

El siguiente ejemplo aplica el perceptrón a datos sintétic… (figura)

Referencias #

Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review, 65(6), 386"・08.
Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.