Máquinas de vectores de soporte (SVM)

Actualizado 2020-03-25 Lectura 3 min

Resumen

SVM aprende una frontera de decisión que maximiza el margen entre clases, priorizando la capacidad de generalización.
El margen blando introduce variables de holgura; el parámetro $C$ controla el equilibrio entre anchura del margen y errores permitidos.
El truco del kernel reemplaza productos internos por funciones kernel, permitiendo fronteras no lineales sin expandir explícitamente las características.
La estandarización de características y la búsqueda de hiperparámetros ($C$, $\gamma$, etc.) son claves para un buen rendimiento.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

Si los datos son separables linealmente, resolvemos

$$ \min_{\mathbf{w}, b} \ \frac{1}{2} \lVert \mathbf{w} \rVert_2^2 \quad \text{s.t.} \quad y_i(\mathbf{w}^\top \mathbf{x}_i + b) \ge 1. $$

En la práctica usamos la variante de margen blando con variables de holgura $\xi_i \ge 0$:

$$ \min_{\mathbf{w}, b, \boldsymbol{\xi}} \ \frac{1}{2} \lVert \mathbf{w} \rVert_2^2 + C \sum_{i=1}^{n} \xi_i \quad \text{s.t.} \quad y_i(\mathbf{w}^\top \mathbf{x}_i + b) \ge 1 - \xi_i. $$

Sustituir los productos internos $\mathbf{x}_i^\top \mathbf{x}_j$ por un kernel $K(\mathbf{x}_i, \mathbf{x}_j)$ permite modelar fronteras no lineales.

Experimentos con Python #

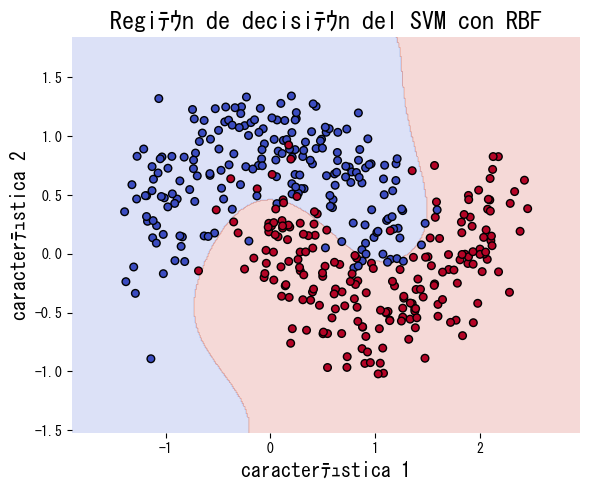
El código siguiente entrena SVM con kernel lineal y con kernel RBF sobre datos generados por make_moons, que no son separables linealmente. El kernel RBF captura la frontera curva con mayor precisión.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_moons
from sklearn.metrics import accuracy_score
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC

def run_svm_demo(
    n_samples: int = 400,
    noise: float = 0.25,
    random_state: int = 42,
    title: str = "Región de decisión del SVM con RBF",
    xlabel: str = "característica 1",
    ylabel: str = "característica 2",
) -> dict[str, float]:
    """Train linear and RBF SVMs and plot the RBF decision boundary."""
    japanize_matplotlib.japanize()
    X, y = make_moons(n_samples=n_samples, noise=noise, random_state=random_state)

    linear_clf = make_pipeline(StandardScaler(), SVC(kernel="linear", C=1.0))
    linear_clf.fit(X, y)

    rbf_clf = make_pipeline(StandardScaler(), SVC(kernel="rbf", C=5.0, gamma=0.5))
    rbf_clf.fit(X, y)

    linear_acc = float(accuracy_score(y, linear_clf.predict(X)))
    rbf_acc = float(accuracy_score(y, rbf_clf.predict(X)))

    grid_x, grid_y = np.meshgrid(
        np.linspace(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, 400),
        np.linspace(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, 400),
    )
    grid = np.c_[grid_x.ravel(), grid_y.ravel()]
    rbf_scores = rbf_clf.predict(grid).reshape(grid_x.shape)

    fig, ax = plt.subplots(figsize=(6, 5))
    ax.contourf(grid_x, grid_y, rbf_scores, alpha=0.2, cmap="coolwarm")
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap="coolwarm", edgecolor="k", s=30)
    ax.set_title(title)
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    fig.tight_layout()
    plt.show()

    return {"linear_accuracy": linear_acc, "rbf_accuracy": rbf_acc}

metrics = run_svm_demo(
    title="Región de decisión del SVM con RBF",
    xlabel="característica 1",
    ylabel="característica 2",
)
print(f"Precisión con kernel lineal: {metrics['linear_accuracy']:.3f}")
print(f"Precisión con kernel RBF: {metrics['rbf_accuracy']:.3f}")

El kernel RBF captura la frontera curva con mayor precisión (figura)

Referencias #

Vapnik, V. (1998). Statistical Learning Theory. Wiley.
Smola, A. J., & Schölkopf, B. (2004). A Tutorial on Support Vector Regression. Statistics and Computing, 14(3), 199"・22.