DBSCAN

Actualizado 2025-11-05 Lectura 4 min

Resumen

DBSCAN agrupa puntos en función de la densidad local, lo que permite detectar formas arbitrarias y dejar las regiones poco densas como ruido.
Dos hiperparámetros dirigen el algoritmo: eps (radio del vecindario) y min_samples (número mínimo de vecinos para declarar un punto como núcleo).
Cada muestra se etiqueta como núcleo, borde o ruido; los clústeres son componentes conectadas de puntos núcleo más los bordes que los tocan.
Una receta habitual es fijar min_samples (≥ dimensión + 1) y barrer eps mientras se observa el porcentaje de puntos que pasan a ruido.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

1. Descripción general #

DBSCAN no necesita conocer cuántos clústeres habrá. Analiza cada punto:

Puntos núcleo: tienen al menos min_samples vecinos a una distancia ≤ eps.
Puntos borde: se encuentran dentro del radio eps de algún núcleo pero no cumplen el criterio por sí mismos.
Ruido: no pertenece al vecindario de ningún núcleo.

Gracias a esta visión basada en densidad, DBSCAN maneja clústeres no convexos (dos lunas, anillos, etc.) y descarta automáticamente zonas dispersas. Escala siempre las variables antes de ajustar.

2. Definición formal #

Para (x_i \in \mathcal{X}), su vecindario (\varepsilon) es

$$ \mathcal{N}_\varepsilon(x_i) = \{ x_j \in \mathcal{X} \mid \lVert x_i - x_j \rVert \le \varepsilon \}. $$

Si (|\mathcal{N}_\varepsilon(x_i)| \ge \texttt{min_samples}|), el punto es núcleo. DBSCAN expande clústeres recorriendo puntos alcanzables por densidad y marca como ruido los no visitados. Con un índice espacial la complejidad es (O(n \log n)).

3. Ejemplo en Python #

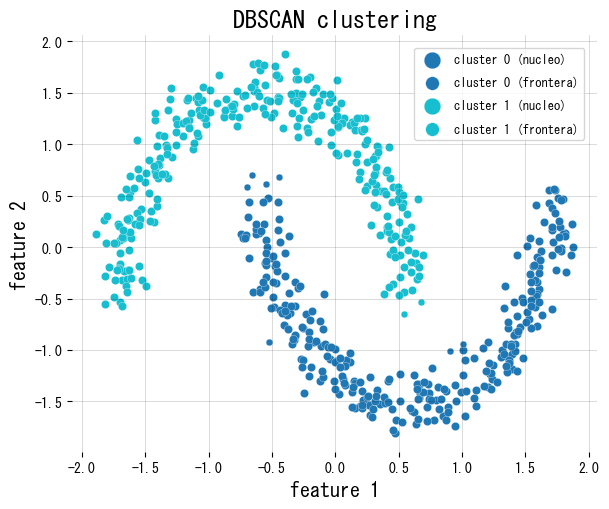
El siguiente script usa scikit-learn para ejecutar DBSCAN sobre un conjunto de dos lunas con ruido, colorea puntos núcleo/borde y reporta cuántos quedan como ruido.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from numpy.typing import NDArray
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
from sklearn.preprocessing import StandardScaler

def run_dbscan_demo(
    n_samples: int = 600,
    noise: float = 0.08,
    eps: float = 0.3,
    min_samples: int = 10,
    random_state: int = 0,
) -> dict[str, int]:
    japanize_matplotlib.japanize()
    features, _ = make_moons(
        n_samples=n_samples,
        noise=noise,
        random_state=random_state,
    )
    features = StandardScaler().fit_transform(features)

    model = DBSCAN(eps=eps, min_samples=min_samples)
    labels = model.fit_predict(features)

    unique_labels = sorted(np.unique(labels))
    cluster_ids = [label for label in unique_labels if label != -1]
    noise_count = int(np.sum(labels == -1))

    core_mask = np.zeros(labels.shape[0], dtype=bool)
    if hasattr(model, "core_sample_indices_"):
        core_mask[model.core_sample_indices_] = True

    fig, ax = plt.subplots(figsize=(6.2, 5.2))
    palette = plt.cm.get_cmap("tab10", max(len(cluster_ids), 1))

    for order, cluster_id in enumerate(cluster_ids):
        mask = labels == cluster_id
        color = palette(order)
        ax.scatter(
            features[mask & core_mask, 0],
            features[mask & core_mask, 1],
            c=[color],
            s=36,
            edgecolor="white",
            linewidth=0.2,
            label=f"Cluster {cluster_id} núcleo",
        )
        ax.scatter(
            features[mask & ~core_mask, 0],
            features[mask & ~core_mask, 1],
            c=[color],
            s=24,
            edgecolor="white",
            linewidth=0.2,
            marker="o",
            label=f"Cluster {cluster_id} borde",
        )

    if noise_count:
        noise_mask = labels == -1
        ax.scatter(
            features[noise_mask, 0],
            features[noise_mask, 1],
            c="#9ca3af",
            marker="x",
            s=28,
            linewidth=0.8,
            label="Ruido",
        )

    ax.set_title("Demostración de DBSCAN")
    ax.set_xlabel("Característica 1")
    ax.set_ylabel("Característica 2")
    ax.grid(alpha=0.2)
    ax.legend(loc="upper right", fontsize=9)
    fig.tight_layout()
    plt.show()

    return {"n_clusters": len(cluster_ids), "n_noise": noise_count}

resultado = run_dbscan_demo()
print(f"Clústeres hallados: {resultado['n_clusters']}")
print(f"Puntos de ruido: {resultado['n_noise']}")

Resultado de DBSCAN

4. Consejos prácticos #

Traza el gráfico de distancias ordenadas al k-ésimo vecino (k = min_samples) y elige eps donde aparezca el codo.
Usa pipelines para estandarizar y agrupar en un mismo paso.
Para conjuntos de datos grandes considera índices de vecinos aproximados o HDBSCAN, que extiende DBSCAN a múltiples densidades y reduce la sensibilidad a eps.

5. Referencias #

Ester, M., Kriegel, H.-P., Sander, J., & Xu, X. (1996). A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. KDD.
Schubert, E., Sander, J., Ester, M., Kriegel, H.-P., & Xu, X. (2017). DBSCAN Revisited, Revisited. ACM Transactions on Database Systems.
scikit-learn developers. (2024). Clustering. https://scikit-learn.org/stable/modules/clustering.html