Modelo de Mezclas Gaussianas (GMM)

Actualizado 2020-03-25 Lectura 3 min

Resumen

Un GMM describe los datos como la suma ponderada de normales multivariadas.
Devuelve una matriz de responsabilidades que cuantifica cuánta probabilidad aporta cada componente a cada muestra.
Los parámetros se estiman con el algoritmo EM; la estructura de covarianzas puede ser full, tied, diag o spherical.
Para elegir el modelo se combinan BIC/AIC con múltiples inicializaciones aleatorias que evitan soluciones inestables.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación #

La densidad de $\mathbf{x}$ es

$$ p(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \, \mathcal{N}(\mathbf{x} \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k), $$

con pesos $\pi_k$ (no negativos y cuya suma es 1). EM alterna:

E-step: cálculo de responsabilidades $\gamma_{ik}$. $$ \gamma_{ik} = \frac{\pi_k \, \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_k, \boldsymbol{\Sigma}_k)} {\sum_{j=1}^K \pi_j \, \mathcal{N}(\mathbf{x}_i \mid \boldsymbol{\mu}_j, \boldsymbol{\Sigma}_j)}. $$
M-step: reestimación de $\pi_k, \boldsymbol{\mu}_k, \boldsymbol{\Sigma}k$ ponderada por $\gamma{ik}$.

La log-verosimilitud aumenta de forma monótona hasta un máximo local.

Ejemplo en Python #

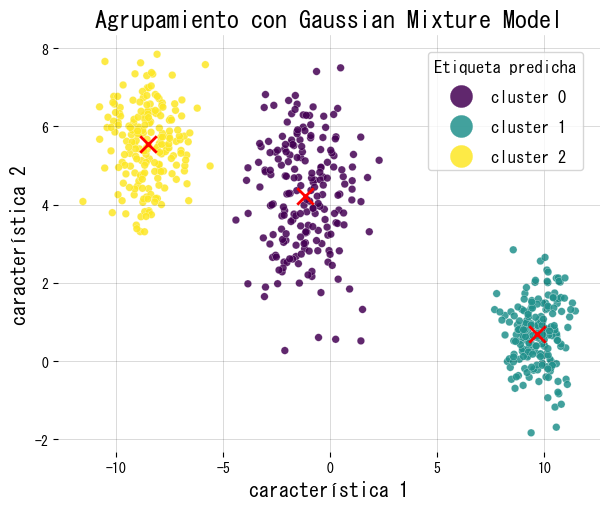
Ajustamos un GMM a datos sintéticos en 2D, representamos las etiquetas duras y mostramos pesos y responsabilidades.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
from numpy.typing import NDArray
from sklearn.datasets import make_blobs
from sklearn.mixture import GaussianMixture

def ejecutar_demo_gmm(
    n_samples: int = 600,
    n_components: int = 3,
    cluster_std: list[float] | tuple[float, ...] = (1.0, 1.4, 0.8),
    covariance_type: str = "full",
    random_state: int = 7,
    n_init: int = 8,
) -> dict[str, object]:
    """Entrena un GMM y visualiza los centros y las etiquetas más probables."""
    caracteristicas, _ = make_blobs(
        n_samples=n_samples,
        centers=n_components,
        cluster_std=cluster_std,
        random_state=random_state,
    )

    gmm = GaussianMixture(
        n_components=n_components,
        covariance_type=covariance_type,
        random_state=random_state,
        n_init=n_init,
    )
    gmm.fit(caracteristicas)

    etiquetas = gmm.predict(caracteristicas)
    responsabilidades = gmm.predict_proba(caracteristicas)
    log_verosimilitud = float(gmm.score(caracteristicas))
    pesos = gmm.weights_

    fig, ax = plt.subplots(figsize=(6.2, 5.2))
    dispersion = ax.scatter(
        caracteristicas[:, 0],
        caracteristicas[:, 1],
        c=etiquetas,
        cmap="viridis",
        s=30,
        edgecolor="white",
        linewidth=0.2,
        alpha=0.85,
    )
    ax.scatter(
        gmm.means_[:, 0],
        gmm.means_[:, 1],
        marker="x",
        c="red",
        s=140,
        linewidth=2.0,
        label="Centro del componente",
    )
    ax.set_title("Agrupamiento con Gaussian Mixture Model")
    ax.set_xlabel("característica 1")
    ax.set_ylabel("característica 2")
    ax.grid(alpha=0.2)
    handles, _ = dispersion.legend_elements()
    etiquetas_legenda = [f"cluster {idx}" for idx in range(n_components)]
    ax.legend(handles, etiquetas_legenda, title="Etiqueta predicha", loc="upper right")
    fig.tight_layout()
    plt.show()

    return {
        "log_likelihood": log_verosimilitud,
        "weights": pesos.tolist(),
        "responsibilities_shape": responsabilidades.shape,
    }

metricas = ejecutar_demo_gmm()
print(f"log-verosimilitud: {metricas['log_likelihood']:.3f}")
print("pesos de mezcla:", metricas["weights"])
print("forma de la matriz de responsabilidades:", metricas["responsibilities_shape"])

Ajustamos un GMM a datos sintéticos en 2D, representamos las… (figura)

Referencias #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Dempster, A. P., Laird, N. M., & Rubin, D. B. (1977). Maximum Likelihood from Incomplete Data via the EM Algorithm. Journal of the Royal Statistical Society, Series B.
scikit-learn developers. (2024). Gaussian Mixture Models. https://scikit-learn.org/stable/modules/mixture.html