PCA

Actualizado 2020-01-29 Lectura 2 min

Resumen

PCA encuentra ejes ortogonales de maxima varianza y proyecta los datos sobre ellos.
La varianza explicada permite elegir cuantas componentes conservar.
La estandarizacion es clave cuando las variables tienen escalas distintas.

Intuicion #

PCA rota el sistema de coordenadas hacia direcciones informativas. Conservando pocos ejes principales se reduce dimension sin perder la estructura dominante.

Explicacion Detallada #

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
from sklearn.datasets import make_blobs

Datos para experimentos #

sklearn.datasets.make_blobs

X, y = make_blobs(n_samples=600, n_features=3, random_state=117117)

fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")

Datos para experimentos (figura)

Reducir la dimensionalidad a dos dimensiones con PCA #

sklearn.decomposition.PCA

from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler

pca = PCA(n_components=2, whiten=True)
X_pca = pca.fit_transform(StandardScaler().fit_transform(X))

fig = plt.figure(figsize=(8, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y)

Reducir la dimensionalidad a dos dimensiones con PCA (figura)

Observar el efecto de la normalización #

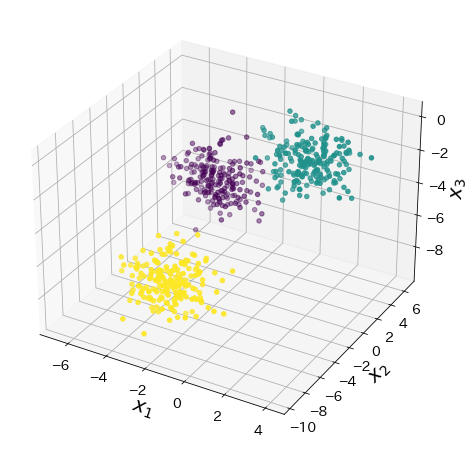
Número de clústeres: 3, con superposición entre clústeres #

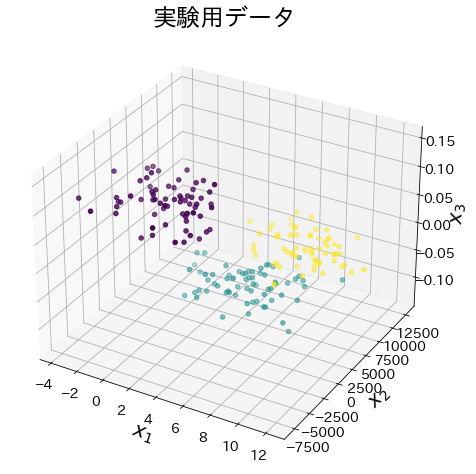
# Datos experimentales
X, y = make_blobs(
    n_samples=200, n_features=3, random_state=11711, centers=3, cluster_std=2.0
)
X[:, 1] = X[:, 1] * 1000
X[:, 2] = X[:, 2] * 0.01
X_ss = StandardScaler().fit_transform(X)

# Graficar los datos originales
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
plt.title("Datos experimentales")
plt.show()

# PCA sin normalización
pca = PCA(n_components=2).fit(X)
X_pca = pca.transform(X)

# PCA con normalización
pca_ss = PCA(n_components=2).fit(X_ss)
X_pca_ss = pca_ss.transform(X_ss)

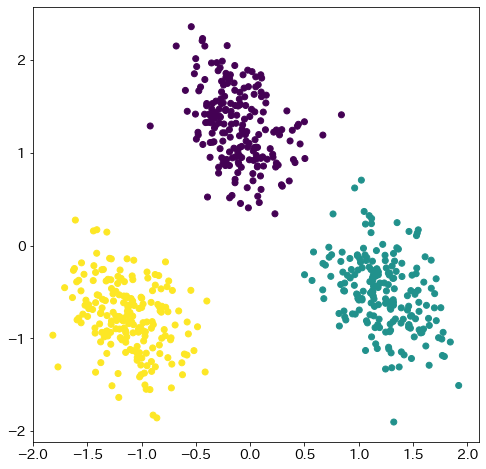
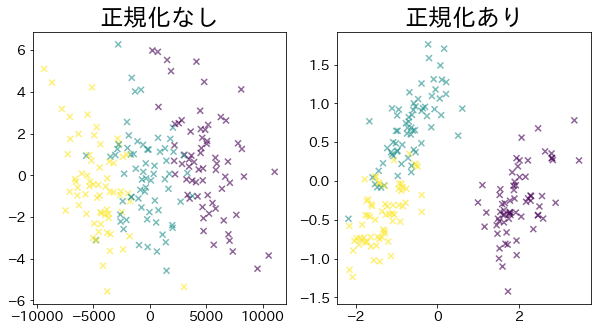
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.title("Sin normalización")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, marker="x", alpha=0.6)
plt.subplot(122)
plt.title("Con normalización")
plt.scatter(X_pca_ss[:, 0], X_pca_ss[:, 1], c=y, marker="x", alpha=0.6)

Número de clústeres: 3, con superposición entre clústeres (figura)

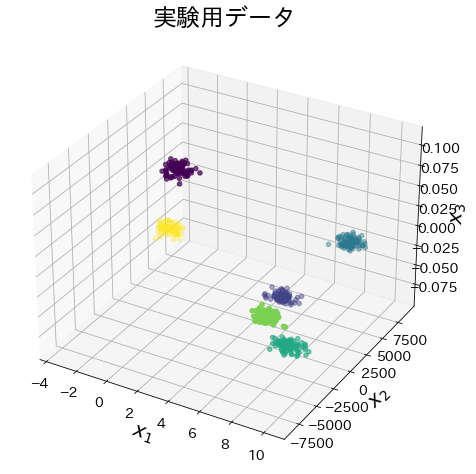
Número de clústeres: 6, sin superposición entre clústeres #

# Datos experimentales
X, y = make_blobs(
    n_samples=500, n_features=3, random_state=11711, centers=6, cluster_std=0.4
)
X[:, 1] = X[:, 1] * 1000
X[:, 2] = X[:, 2] * 0.01
X_ss = StandardScaler().fit_transform(X)

# Graficar los datos originales
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(projection="3d")
ax.scatter(X[:, 0], X[:, 1], X[:, 2], marker="o", c=y)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$x_3$")
plt.title("Datos experimentales")
plt.show()

# PCA sin normalización
pca = PCA(n_components=2).fit(X)
X_pca = pca.transform(X)

# PCA con normalización
pca_ss = PCA(n_components=2).fit(X_ss)
X_pca_ss = pca_ss.transform(X_ss)

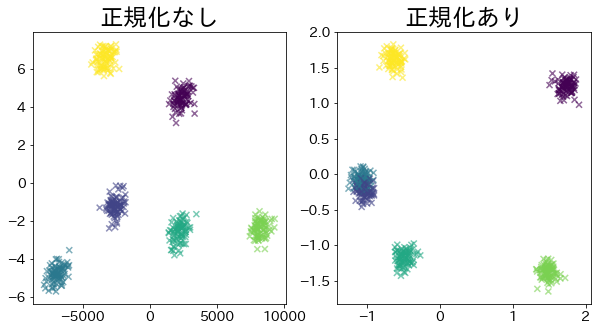
fig = plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.title("Sin normalización")
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, marker="x", alpha=0.6)
plt.subplot(122)
plt.title("Con normalización")
plt.scatter(X_pca_ss[:, 0], X_pca_ss[:, 1], c=y, marker="x", alpha=0.6)

Número de clústeres: 6, sin superposición entre clústeres (figura)