Regresión lineal bayesiana

Actualizado 2020-04-08 Lectura 4 min

Resumen

La regresión lineal bayesiana trata los coeficientes como variables aleatorias y estima simultáneamente las predicciones y su incertidumbre.
La distribución posterior se obtiene de forma analítica a partir de la distribución previa y la verosimilitud, lo que la hace robusta con pocos datos o mucho ruido.
La distribución predictiva es gaussiana, de modo que su media y varianza se pueden visualizar para apoyar la toma de decisiones.
BayesianRidge en scikit-learn ajusta automáticamente la varianza del ruido y facilita el uso práctico del método.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

Suponemos una distribución previa gaussiana multivariante de media 0 y varianza $\tau^{-1}$ para el vector de coeficientes $\boldsymbol\beta$, y ruido gaussiano $\epsilon_i \sim \mathcal{N}(0, \alpha^{-1})$ en las observaciones. La posterior resulta ser

$$ p(\boldsymbol\beta \mid \mathbf{X}, \mathbf{y}) = \mathcal{N}(\boldsymbol\beta \mid \boldsymbol\mu, \mathbf{\Sigma}) $$

con

$$ \mathbf{\Sigma} = (\alpha \mathbf{X}^\top \mathbf{X} + \tau \mathbf{I})^{-1}, \qquad \boldsymbol\mu = \alpha \mathbf{\Sigma} \mathbf{X}^\top \mathbf{y}. $$

La distribución predictiva para una nueva entrada $\mathbf{x}*$ también es gaussiana, $\mathcal{N}(\hat{y}, \sigma_^2)$. BayesianRidge estima $\alpha$ y $\tau$ a partir de los datos, evitando un ajuste manual.

Experimentos con Python #

El ejemplo siguiente compara mínimos cuadrados ordinarios con la regresión lineal bayesiana en presencia de valores atípicos.

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import BayesianRidge, LinearRegression
from sklearn.metrics import mean_squared_error

def run_bayesian_linear_demo(
    n_samples: int = 120,
    noise_scale: float = 1.0,
    outlier_count: int = 6,
    outlier_scale: float = 8.0,
    label_observations: str = "observations",
    label_ols: str = "OLS",
    label_bayes: str = "Bayesian mean",
    label_interval: str = "95% CI",
    xlabel: str = "input $",
    ylabel: str = "output $",
    title: str | None = None,
) -> dict[str, float]:
    """Fit OLS and Bayesian ridge to noisy data with outliers, plotting results.

    Args:
        n_samples: Number of evenly spaced sample points.
        noise_scale: Standard deviation of Gaussian noise added to the base line.
        outlier_count: Number of indices to perturb strongly.
        outlier_scale: Standard deviation for the outlier noise.
        label_observations: Legend label for observations.
        label_ols: Label for the ordinary least squares line.
        label_bayes: Label for the Bayesian posterior mean line.
        label_interval: Label for the confidence interval band.
        xlabel: X-axis label.
        ylabel: Y-axis label.
        title: Optional plot title.

    Returns:
        Dictionary containing MSEs and coefficients statistics.
    """
    japanize_matplotlib.japanize()
    rng = np.random.default_rng(seed=0)

    x_values: np.ndarray = np.linspace(-4.0, 4.0, n_samples, dtype=float)
    y_clean: np.ndarray = 1.8 * x_values - 0.5
    y_noisy: np.ndarray = y_clean + rng.normal(scale=noise_scale, size=x_values.shape)

    outlier_idx = rng.choice(n_samples, size=outlier_count, replace=False)
    y_noisy[outlier_idx] += rng.normal(scale=outlier_scale, size=outlier_idx.shape)

    X: np.ndarray = x_values[:, np.newaxis]

    ols = LinearRegression()
    ols.fit(X, y_noisy)
    bayes = BayesianRidge(compute_score=True)
    bayes.fit(X, y_noisy)

    X_grid: np.ndarray = np.linspace(-6.0, 6.0, 200, dtype=float)[:, np.newaxis]
    ols_mean: np.ndarray = ols.predict(X_grid)
    bayes_mean, bayes_std = bayes.predict(X_grid, return_std=True)

    metrics = {
        "ols_mse": float(mean_squared_error(y_noisy, ols.predict(X))),
        "bayes_mse": float(mean_squared_error(y_noisy, bayes.predict(X))),
        "coef_mean": float(bayes.coef_[0]),
        "coef_std": float(np.sqrt(bayes.sigma_[0, 0])),
    }

    upper = bayes_mean + 1.96 * bayes_std
    lower = bayes_mean - 1.96 * bayes_std

    fig, ax = plt.subplots(figsize=(10, 5))
    ax.scatter(X, y_noisy, color="#ff7f0e", alpha=0.6, label=label_observations)
    ax.plot(X_grid, ols_mean, color="#1f77b4", linestyle="--", label=label_ols)
    ax.plot(X_grid, bayes_mean, color="#2ca02c", linewidth=2, label=label_bayes)
    ax.fill_between(
        X_grid.ravel(),
        lower,
        upper,
        color="#2ca02c",
        alpha=0.2,
        label=label_interval,
    )
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return metrics

metrics = run_bayesian_linear_demo(
    label_observations="observaciones",
    label_ols="MCO",
    label_bayes="Media bayesiana",
    label_interval="IC del 95%",
    xlabel="entrada $",
    ylabel="salida $",
    title="Regresión bayesiana vs. OLS",
)
print(f"MSE de OLS: {metrics['ols_mse']:.3f}")
print(f"MSE de la regresión bayesiana: {metrics['bayes_mse']:.3f}")
print(f"Media posterior del coeficiente: {metrics['coef_mean']:.3f}")
print(f"Desviación estándar posterior: {metrics['coef_std']:.3f}")

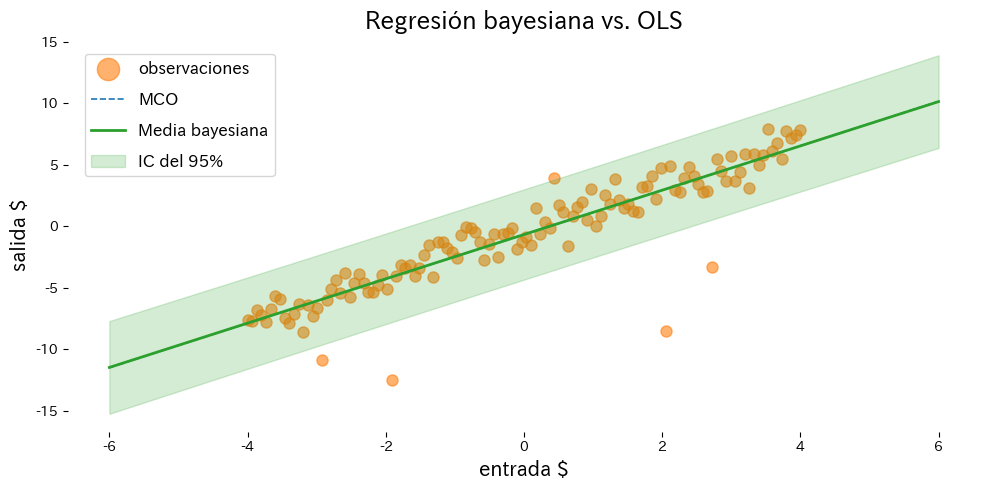
El ejemplo siguiente compara mínimos cuadrados ordinarios co… (figura)

Interpretación de los resultados #

OLS se ve arrastrado por los outliers, mientras que la regresión bayesiana mantiene más estable la predicción media.
return_std=True devuelve la desviación estándar predictiva y permite trazar intervalos creíbles con facilidad.
La varianza posterior revela qué coeficientes conservan mayor incertidumbre.

Referencias #

Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.
Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. MIT Press.