Regresión por componentes principales (PCR)

Actualizado 2020-05-06 Lectura 3 min

Resumen

PCR aplica PCA para comprimir las características antes de ajustar la regresión lineal, reduciendo la inestabilidad causada por la multicolinealidad.
Los componentes principales priorizan las direcciones con mayor varianza, filtrando el ruido y preservando la estructura informativa.
Elegir cuántos componentes conservar permite equilibrar el riesgo de sobreajuste y el coste computacional.
Un buen preprocesamiento —estandarización y tratamiento de valores perdidos— sienta las bases para un modelo preciso e interpretable.

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

Formulación matemática #

Aplicamos PCA a la matriz de diseño estandarizada $\mathbf{X}$ y conservamos los $k$ autovectores principales. Con las puntuaciones $\mathbf{Z} = \mathbf{X} \mathbf{W}_k$, el modelo de regresión

$$ y = \boldsymbol{\gamma}^\top \mathbf{Z} + b $$

se ajusta a los datos. Los coeficientes en el espacio original se recuperan mediante $\boldsymbol{\beta} = \mathbf{W}_k \boldsymbol{\gamma}$. El número de componentes $k$ se elige usando la varianza explicada acumulada o validación cruzada.

Experimentos con Python #

Evaluamos la regresión PCR en el conjunto de datos de diabetes variando el número de componentes y midiendo el desempeño con validación cruzada.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
from __future__ import annotations

import japanize_matplotlib
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_diabetes
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def evaluate_pcr_components(
    cv_folds: int = 5,
    xlabel: str = "Number of components k",
    ylabel: str = "CV MSE (lower is better)",
    title: str | None = None,
    label_best: str = "best={k}",
) -> dict[str, float]:
    """Cross-validate PCR with varying component counts and plot the curve.

    Args:
        cv_folds: Number of folds for cross-validation.
        xlabel: Label for the component-count axis.
        ylabel: Label for the error axis.
        title: Optional title for the plot.
        label_best: Format string for highlighting the best component count.

    Returns:
        Dictionary containing the best component count and its CV score.
    """
    japanize_matplotlib.japanize()
    X, y = load_diabetes(return_X_y=True)

    def build_pcr(n_components: int) -> Pipeline:
        return Pipeline([
            ("scale", StandardScaler()),
            ("pca", PCA(n_components=n_components, random_state=0)),
            ("reg", LinearRegression()),
        ])

    components = np.arange(1, X.shape[1] + 1)
    cv_scores = []
    for k in components:
        model = build_pcr(int(k))
        score = cross_val_score(
            model,
            X,
            y,
            cv=cv_folds,
            scoring="neg_mean_squared_error",
        )
        cv_scores.append(score.mean())

    cv_scores_arr = np.array(cv_scores)
    best_idx = int(np.argmax(cv_scores_arr))
    best_k = int(components[best_idx])
    best_mse = float(-cv_scores_arr[best_idx])

    best_model = build_pcr(best_k).fit(X, y)
    explained = best_model["pca"].explained_variance_ratio_

    fig, ax = plt.subplots(figsize=(8, 4))
    ax.plot(components, -cv_scores_arr, marker="o")
    ax.axvline(best_k, color="red", linestyle="--", label=label_best.format(k=best_k))
    ax.set_xlabel(xlabel)
    ax.set_ylabel(ylabel)
    if title:
        ax.set_title(title)
    ax.legend()
    fig.tight_layout()
    plt.show()

    return {
        "best_k": best_k,
        "best_mse": best_mse,
        "explained_variance_ratio": explained,
    }

metrics = evaluate_pcr_components(
    xlabel="Número de componentes k",
    ylabel="MSE de CV (más bajo es mejor)",
    title="PCR y número de componentes",
    label_best="mejor k={k}",
)
print(f"Mejor número de componentes: {metrics['best_k']}")
print(f"Mejor MSE de CV: {metrics['best_mse']:.3f}")
print("Proporción de varianza explicada:", metrics['explained_variance_ratio'])

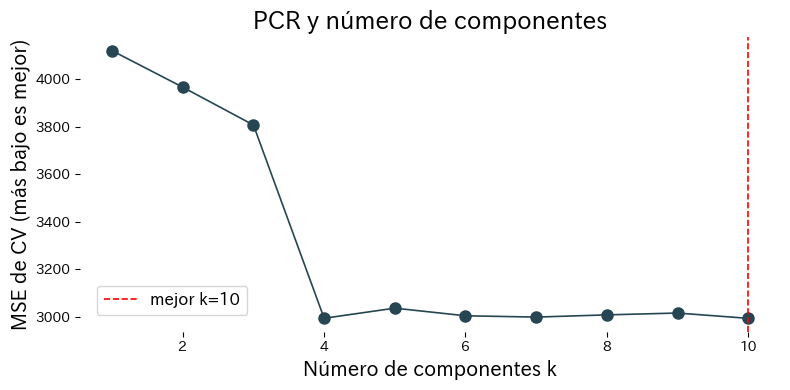
Evaluamos la regresión PCR en el conjunto de datos de diabet… (figura)

Interpretación de los resultados #

Al aumentar los componentes, el ajuste sobre el entrenamiento mejora, pero el MSE de validación cruzada alcanza un mínimo intermedio.
La proporción de varianza explicada indica cuánta variabilidad captura cada componente.
Analizar los loadings muestra qué características originales contribuyen más a cada dirección principal.

Referencias #

Jolliffe, I. T. (2002). Principal Component Analysis (2nd ed.). Springer.
Massy, W. F. (1965). Principal Components Regression in Exploratory Statistical Research. Journal of the American Statistical Association, 60(309), 234–256.