- Un árbol de decisión para clasificación divide el espacio de características con una secuencia de preguntas if-then hasta que cada hoja contenga casi una sola clase.
- La calidad de cada división se evalúa con medidas de impureza como el índice de Gini o la entropía; elija la que mejor refleje el costo de clasificar mal en su problema.
- Limitar la profundidad, exigir un mínimo de muestras por nodo o aplicar poda evita que el árbol memorice ruido y mantiene la interpretabilidad.
- Visualizar las regiones de decisión y la estructura del árbol facilita explicar el modelo a las partes interesadas.
1. Descripción general #
Los árboles de decisión son modelos supervisados que separan el espacio de entrada de forma recursiva. Cada nodo interno plantea una pregunta del tipo “¿(x_j \le s)?”. Para clasificación buscamos hojas puras, es decir, con una sola etiqueta predominante. El resultado es un conjunto compacto de reglas que puede convertirse en políticas de negocio con facilidad.
2. Medidas de impureza #
Sea (t) un nodo y (p_k) la proporción de la clase (k) dentro de él. Las medidas más usadas son
$$ \mathrm{Gini}(t) = 1 - \sum_k p_k^2, $$
$$ H(t) = - \sum_k p_k \log p_k. $$
Si dividimos el nodo (t) con la característica (x_j) y el umbral (s), evaluamos la ganancia
$$ \Delta I = I(t) - \frac{n_L}{n_t} I(t_L) - \frac{n_R}{n_t} I(t_R), $$
donde (I(\cdot)) es Gini o entropía, (t_L) y (t_R) son los nodos hijo y (n_t) es la cantidad de muestras que llega a (t). Elegimos la división que maximiza (\Delta I).
3. Ejemplo en Python #
El siguiente código crea un conjunto de datos sintético de dos clases con make_classification, entrena DecisionTreeClassifier y dibuja sus regiones de decisión. Cambiar criterion="gini" por "entropy" permite probar otra medida de impureza.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.tree import DecisionTreeClassifier, plot_tree
n_classes = 2
X, y = make_classification(
n_samples=100,
n_features=2,
n_redundant=0,
n_informative=2,
random_state=2,
n_classes=n_classes,
n_clusters_per_class=1,
)
clf = DecisionTreeClassifier(criterion="gini", random_state=0).fit(X, y)
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(
np.arange(x_min, x_max, 0.1),
np.arange(y_min, y_max, 0.1),
)
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.figure(figsize=(8, 8))
plt.contourf(xx, yy, Z, cmap=plt.cm.Pastel1, alpha=0.6)
plt.xlabel("x1")
plt.ylabel("x2")
for i, color, label_name in zip(range(n_classes), ["r", "b"], ["A", "B"]):
idx = np.where(y == i)
plt.scatter(X[idx, 0], X[idx, 1], c=color, label=label_name, edgecolor="k")
plt.legend()
plt.title("Regiones de decisión generadas por el árbol")
plt.show()
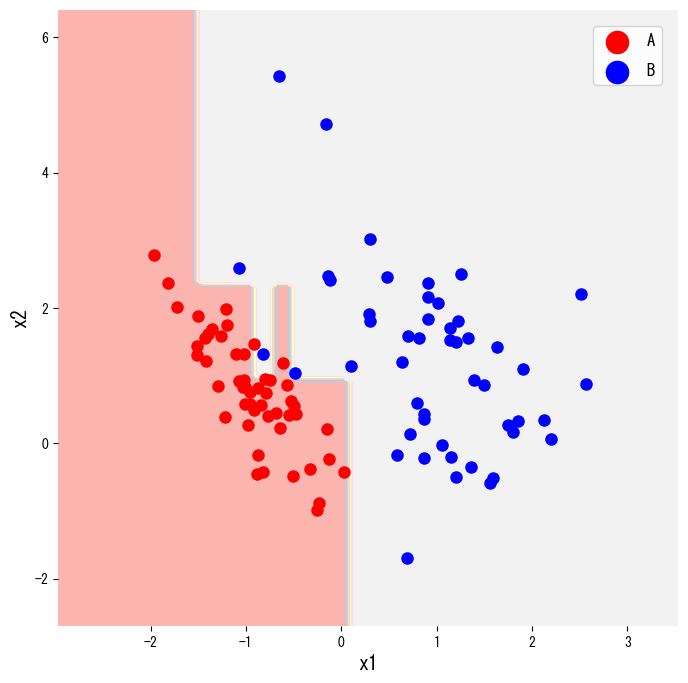
También podemos representar el árbol completo con plot_tree, útil para informes o presentaciones.
plt.figure(figsize=(12, 12))
plot_tree(clf, filled=True, feature_names=["x1", "x2"], class_names=["A", "B"])
plt.show()
4. Referencias #
- Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
- scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html