- Los árboles de regresión aproximan relaciones no lineales dividiendo recursivamente el espacio de características hasta que cada hoja pueda representarse con un valor constante.
- Las divisiones minimizan el error cuadrático medio (MSE) de los nodos hijos; la reducción de MSE indica si una pregunta aporta valor.
- Hiperparámetros como
max_depth,min_samples_leafyccp_alphaequilibran precisión e interpretabilidad y ayudan a evitar sobreajuste. - Gráficos de dispersión, mapas de contorno y árboles renderizados facilitan explicar qué regiones comparten la misma predicción.
1. Descripción general #
Al igual que en clasificación, los árboles de regresión formulan preguntas sencillas sobre las variables de entrada, pero ahora el objetivo es continuo. Cada hoja predice la media de los ejemplos que llegan a ella, por lo que la función resultante es constante a trozos. Cuanto mayor sea la profundidad, mayor detalle capturará el modelo; árboles poco profundos priorizan tendencias suaves.
2. Criterio de división (reducción de varianza) #
Para un nodo (t) con (n_t) observaciones y media (\bar{y}_t), la impureza se define como
$$ \mathrm{MSE}(t) = \frac{1}{n_t} \sum_{i \in t} (y_i - \bar{y}_t)^2. $$
Si dividimos (t) usando la característica (x_j) y el umbral (s), la ganancia viene dada por
$$ \Delta = \mathrm{MSE}(t) - \frac{n_L}{n_t} \mathrm{MSE}(t_L) - \frac{n_R}{n_t} \mathrm{MSE}(t_R). $$
Elegimos la división que maximiza (\Delta); cuando ninguna mejora la impureza, el nodo se convierte en hoja.
3. Ejemplo en Python #
El primer bloque ajusta un árbol superficial a muestras ruidosas de una curva seno para mostrar el carácter por tramos. El segundo experimento entrena un regresor con dos variables, calcula (R^2), RMSE y MAE, y visualiza la superficie aprendida junto con el árbol final.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor, plot_tree
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
rng = np.random.default_rng(42)
X1 = np.sort(5 * rng.random((120, 1)), axis=0)
y1_true = np.sin(X1).ravel()
y1 = y1_true + rng.normal(scale=0.2, size=X1.shape[0])
reg1 = DecisionTreeRegressor(max_depth=3, random_state=0).fit(X1, y1)
y1_pred = reg1.predict(X1)
plt.figure(figsize=(8, 4))
plt.scatter(X1, y1, s=15, c="gray", label="observaciones")
plt.plot(X1, y1_true, lw=2, label="señal real")
plt.step(X1.ravel(), y1_pred, where="mid", lw=2, label="predicción del árbol")
plt.xlabel("x")
plt.ylabel("y")
plt.title("Ajuste por tramos de un árbol de regresión")
plt.legend()
plt.grid(alpha=0.3)
plt.show()
X, y = make_regression(n_samples=400, n_features=2, noise=15.0, random_state=777)
reg = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)
r2 = r2_score(y, reg.predict(X))
rmse = mean_squared_error(y, reg.predict(X), squared=False)
mae = mean_absolute_error(y, reg.predict(X))
print(f"R2={r2:.3f} RMSE={rmse:.2f} MAE={mae:.2f}")
x_min, x_max = X[:, 0].min()-1, X[:, 0].max()+1
y_min, y_max = X[:, 1].min()-1, X[:, 1].max()+1
xx, yy = np.meshgrid(
np.linspace(x_min, x_max, 150),
np.linspace(y_min, y_max, 150),
)
zz = reg.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.figure(figsize=(7, 6))
cs = plt.contourf(xx, yy, zz, levels=15, cmap="viridis", alpha=0.8)
plt.colorbar(cs, label="predicción")
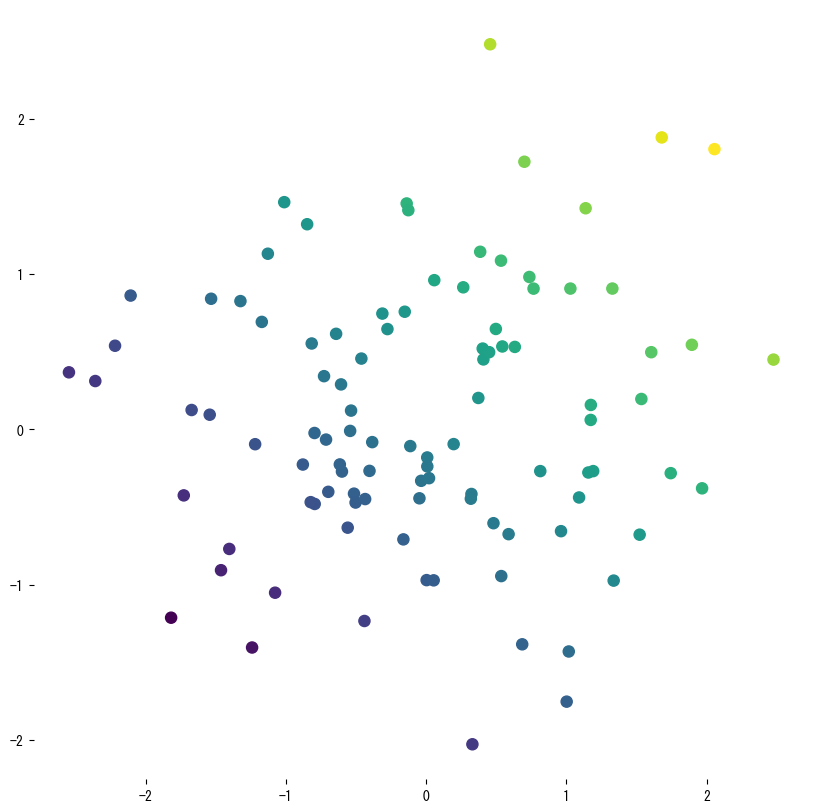
plt.scatter(X[:, 0], X[:, 1], c=y, cmap="viridis", s=20, edgecolor="k", alpha=0.7)
plt.xlabel("x1")
plt.ylabel("x2")
plt.title("Superficie de predicción del árbol")
plt.show()
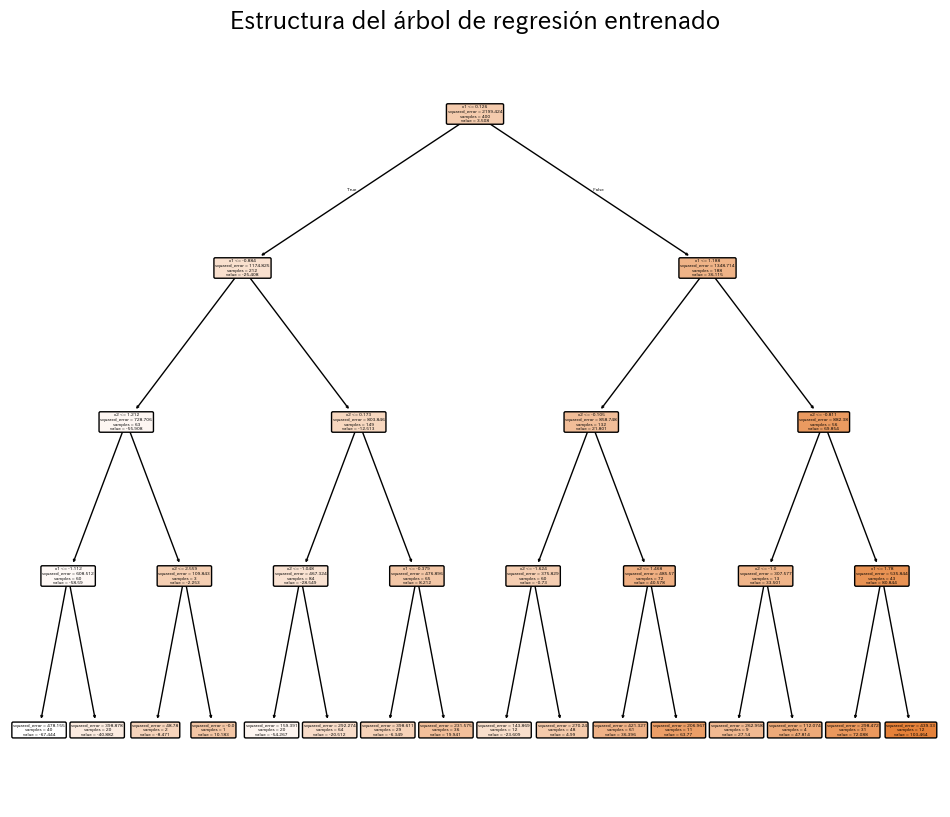
plt.figure(figsize=(12, 10))
plot_tree(
reg,
filled=True,
feature_names=["x1", "x2"],
rounded=True,
)
plt.title("Estructura del árbol de regresión entrenado")
plt.show()
4. Referencias #
- Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and Regression Trees. Wadsworth.
- scikit-learn developers. (2024). Decision Trees. https://scikit-learn.org/stable/modules/tree.html