Parámetros del árbol

Intuicion #

Este metodo se entiende mejor al conectar sus supuestos con la estructura de los datos y su efecto en la generalizacion.

Explicacion Detallada #

1. Descripción general #

Sin restricciones, un árbol sigue dividiendo hasta dejar hojas totalmente puras, lo que suele implicar sobreajuste. Los hiperparámetros actúan como regularizadores: la profundidad impide que el árbol sea demasiado detallado, las muestras mínimas evitan hojas minúsculas y la poda colapsa ramas marginales.

2. Ganancia de impureza y poda por complejidad #

Para un nodo padre (P) que se divide en hijos (L) y (R), la reducción de impureza es

donde (I(\cdot)) puede ser Gini, entropía, MSE o MAE. Sólo mantenemos divisiones con (\Delta I > 0).

La poda por complejidad evalúa un árbol (T) mediante

donde (R(T)) es la pérdida de entrenamiento, (|T|) el número de hojas y (\alpha \ge 0) penaliza estructuras grandes. Aumentar (\alpha) conduce a árboles más simples.

3. Experimentos en Python #

El siguiente código entrena varios DecisionTreeRegressor sobre un conjunto sintético y muestra cómo distintos parámetros afectan el (R^2) de entrenamiento y prueba.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeRegressor
from sklearn.datasets import make_regression
from sklearn.metrics import r2_score

X, y = make_regression(
    n_samples=500,
    n_features=2,
    noise=0.2,
    random_state=42,
)
Xtr, Xte, ytr, yte = train_test_split(X, y, test_size=0.3, random_state=0)

def evaluate(params):
    model = DecisionTreeRegressor(random_state=0, **params).fit(Xtr, ytr)
    r2_train = r2_score(ytr, model.predict(Xtr))
    r2_test = r2_score(yte, model.predict(Xte))
    print(f"{params}: train R2={r2_train:.3f}, test R2={r2_test:.3f}")

evaluate({"max_depth": 3})
evaluate({"max_depth": 10})
evaluate({"max_depth": 5, "min_samples_leaf": 5})
evaluate({"max_depth": 5, "ccp_alpha": 0.01})

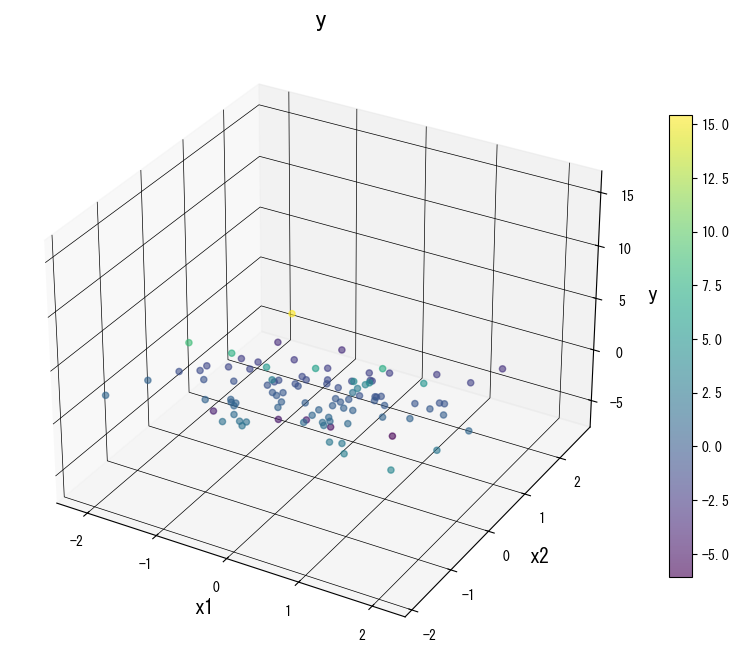
Las siguientes figuras muestran cómo cambia la superficie de predicción al modificar los parámetros clave:

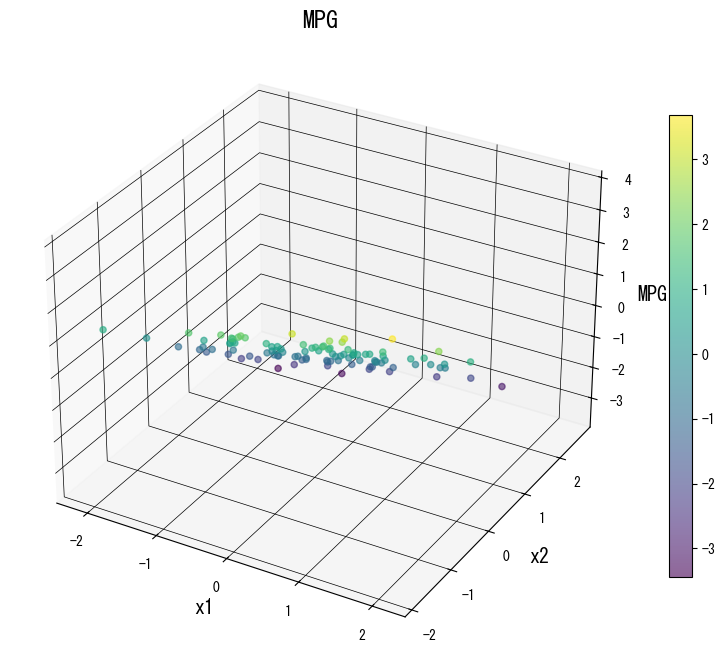
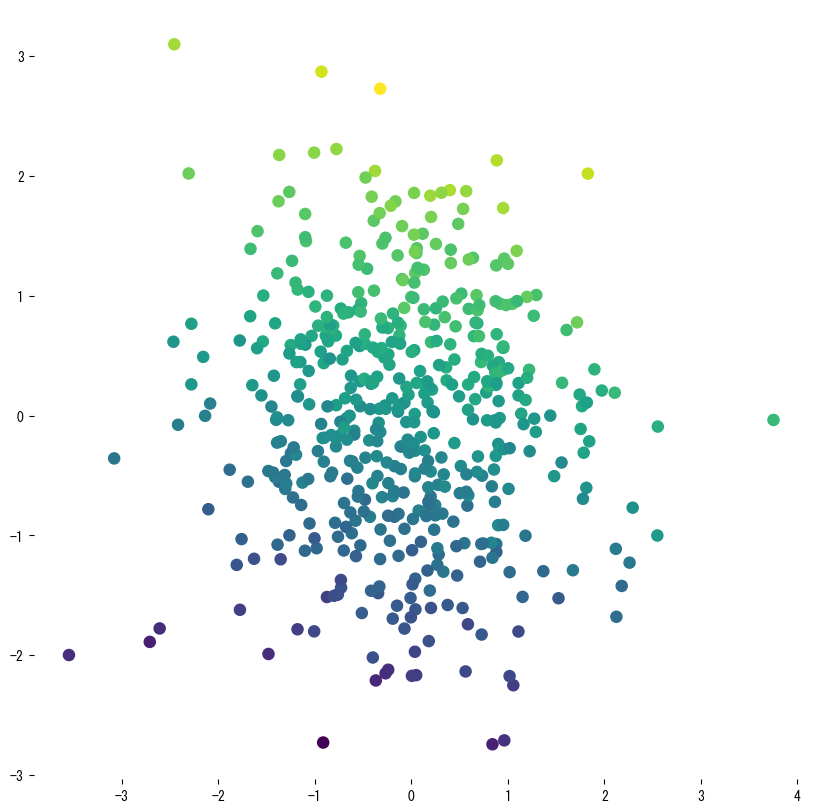
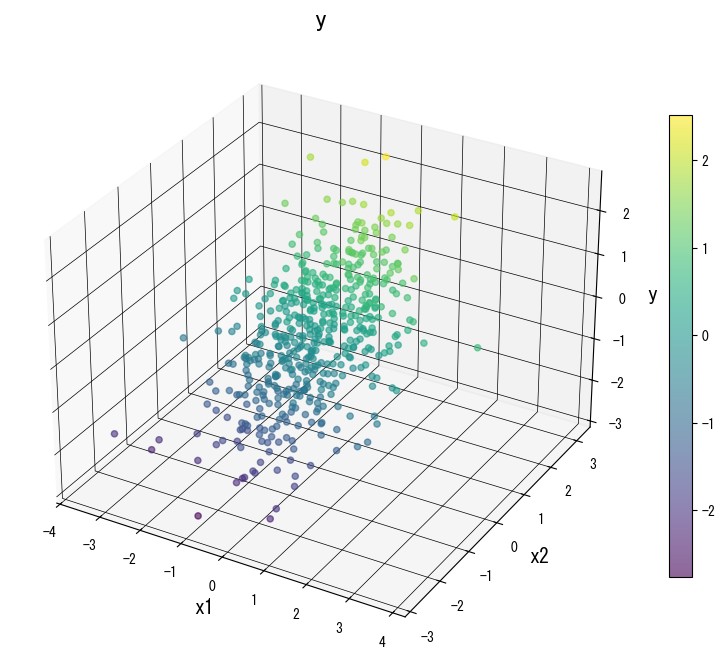
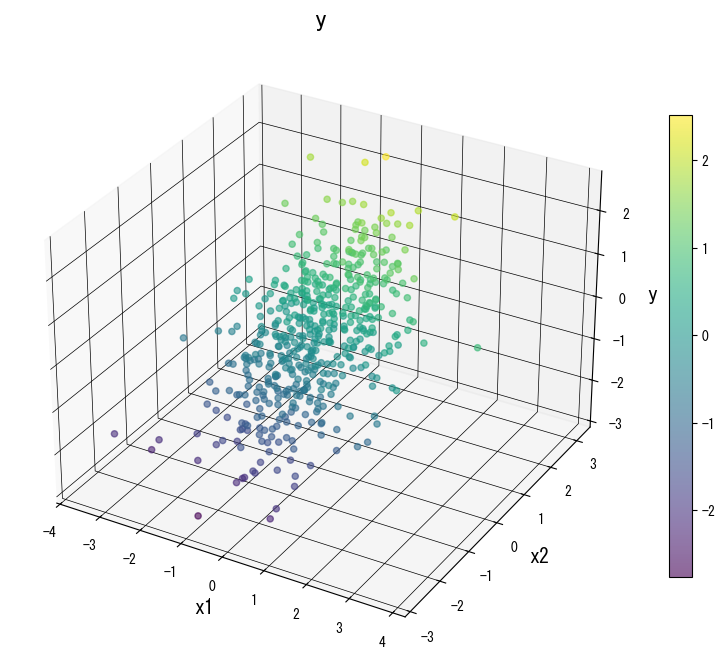
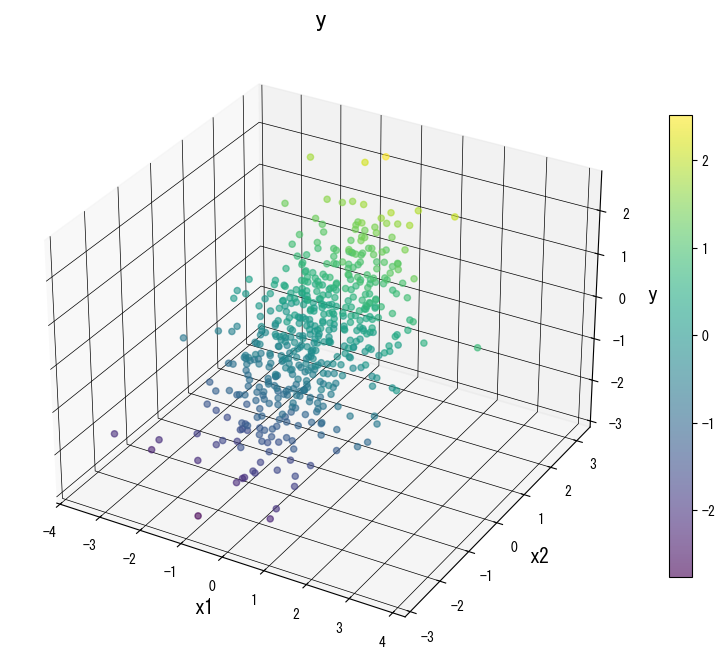
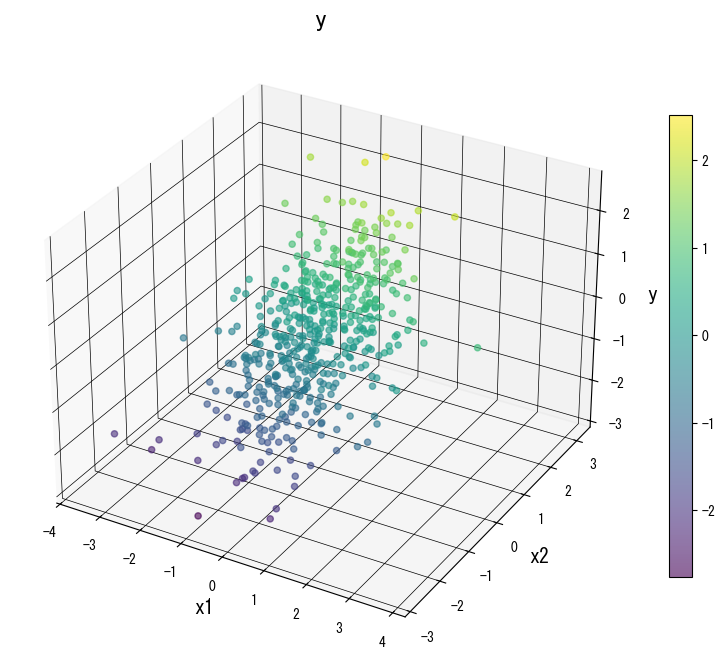
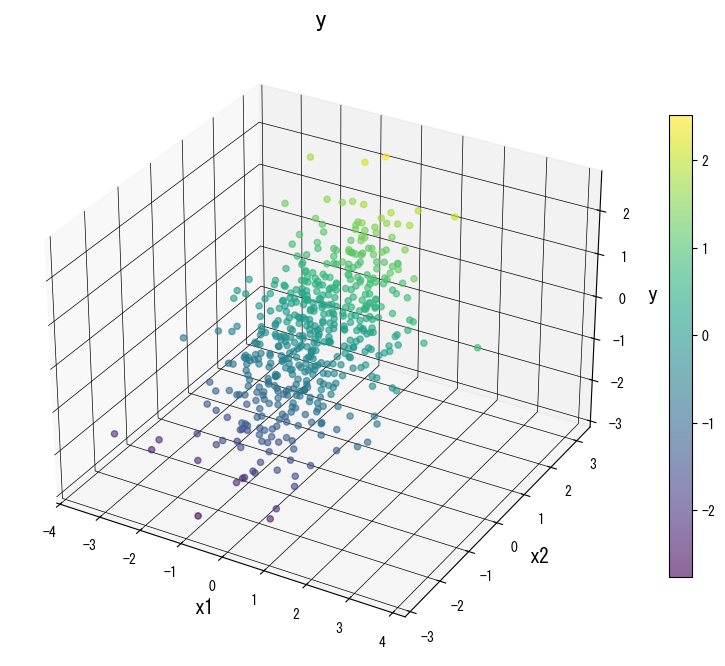
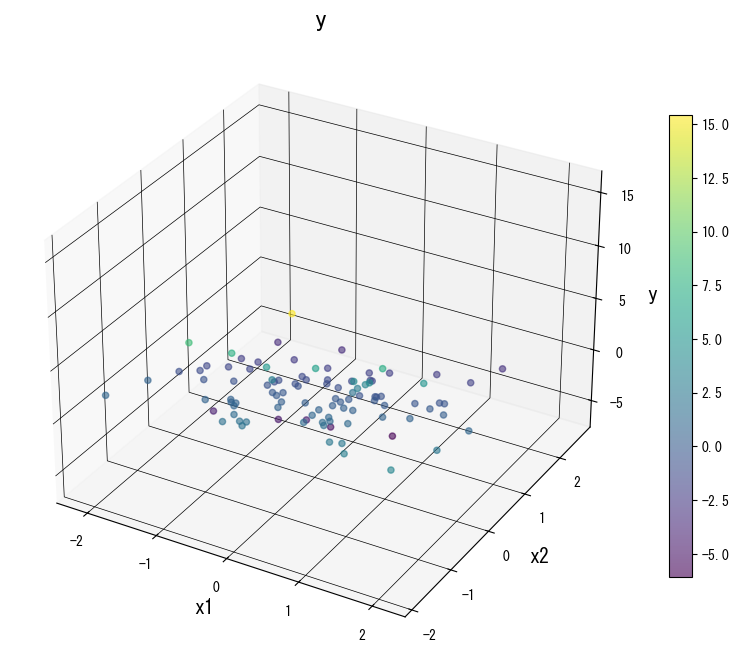
4. Referencias #