Curva de validación

Eval

Curva de validación

Creado: Última actualización: Tiempo de lectura: 3 min
まとめ
  • Las curvas de validación muestran cómo cambian las métricas de entrenamiento y validación al variar un hiperparámetro.
  • Utiliza validation_curve para barrer el coeficiente de regularización, graficar ambas curvas y localizar el punto óptimo.
  • Aprende a leer la gráfica durante el tuning y qué precauciones conviene tener en cuenta.

sklearn.model_selection.validation_curve

1. ¿Qué es una curva de validación? #

Representa en el eje X un hiperparámetro y en el eje Y las puntuaciones de entrenamiento y validación. Interpretación típica:

  • Entrenamiento alto, validación baja → sobreajuste; incrementa la regularización o reduce la complejidad.
  • Ambos bajos → infraajuste; relaja la regularización o emplea un modelo más expresivo.
  • Ambos altos y cercanos → configuración prometedora; confirma con otras métricas.

Mientras que una curva de aprendizaje analiza “tamaño de muestra vs. puntuación”, la curva de validación estudia “hiperparámetro vs. puntuación”.

2. Ejemplo en Python (SVC con C) #

from __future__ import annotations

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import validation_curve
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC


def plot_validation_curve_for_svc() -> None:
    """Dibuja y guarda la curva de validación para el parámetro C de SVC."""
    features, labels = make_classification(
        n_samples=1200,
        n_features=20,
        n_informative=5,
        n_redundant=2,
        n_repeated=0,
        n_classes=2,
        weights=[0.6, 0.4],
        flip_y=0.02,
        class_sep=1.2,
        random_state=42,
    )

    model = make_pipeline(StandardScaler(), SVC(kernel="rbf", gamma="scale"))
    param_range = np.logspace(-3, 2, 10)

    train_scores, valid_scores = validation_curve(
        estimator=model,
        X=features,
        y=labels,
        param_name="svc__C",
        param_range=param_range,
        scoring="roc_auc",
        cv=5,
        n_jobs=None,
    )

    train_mean = train_scores.mean(axis=1)
    train_std = train_scores.std(axis=1)
    valid_mean = valid_scores.mean(axis=1)
    valid_std = valid_scores.std(axis=1)

    plt.figure(figsize=(7, 5))
    plt.semilogx(param_range, train_mean, label="Train score", color="#1d4ed8")
    plt.fill_between(
        param_range,
        train_mean - train_std,
        train_mean + train_std,
        alpha=0.2,
        color="#1d4ed8",
    )
    plt.semilogx(param_range, valid_mean, label="Validation score", color="#ea580c")
    plt.fill_between(
        param_range,
        valid_mean - valid_std,
        valid_mean + valid_std,
        alpha=0.2,
        color="#ea580c",
    )
    plt.title("Validation Curve for SVC (ROC-AUC)")
    plt.xlabel("Parámetro de regularización C")
    plt.ylabel("Puntuación")
    plt.ylim(0.5, 1.05)
    plt.legend(loc="best")
    plt.grid(alpha=0.3)


plot_validation_curve_for_svc()
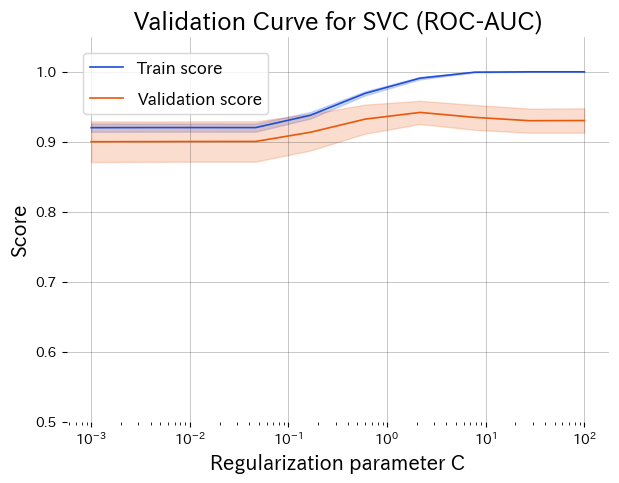
Curva de validación para SVC

Valores bajos de C producen infraajuste; valores altos generan sobreajuste. Alrededor de C ≈ 1 se alcanza el mejor equilibrio.

3. Cómo leer la gráfica #

  • Parte izquierda (C pequeño): regularización fuerte → infraajuste, ambas curvas bajas.
  • Parte derecha (C grande): regularización débil → la curva de entrenamiento sube y la de validación cae.
  • Pico central: las curvas convergen y alcanzan su máximo; candidatos a valor óptimo.

4. Uso práctico #

  • Exploración previa: delimita un rango razonable antes de lanzar búsquedas costosas (grid, random, bayesiana).
  • Revisa la varianza: atiende a las bandas sombreadas (desviación típica), sobre todo con pocos datos.
  • Prioriza hiperparámetros: genera curvas para los parámetros clave y decide cuáles merecen tuning exhaustivo.
  • Combínalas con curvas de aprendizaje: entiende qué hiperparámetro funciona y si conviene recolectar más datos.

Las curvas de validación aportan intuición sobre la dirección del ajuste y facilitan explicar decisiones al resto del equipo. Guardar estos gráficos por modelo simplifica la discusión de mejoras futuras.