4.2.1
Coeficiente de correlación
- Coeficiente de correlaciónの概要を押さえ、評価対象と読み取り方を整理します。
- Python 3.13 のコード例で算出・可視化し、手順と実務での確認ポイントを確認します。
- 図表や補助指標を組み合わせ、モデル比較や閾値調整に活かすヒントをまとめます。
El coeficiente de correlación mide la fuerza de una relación lineal entre dos datos o variables aleatorias.
Es un indicador que permite comprobar si existe un cambio de tendencia de forma lineal entre dos variables, que puede expresarse en la siguiente ecuación.
$
\frac{\Sigma_{i=1}^N (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\Sigma_{i=1}^N(x_i - \bar{x})^2 \Sigma_{i=1}^N(y_i - \bar{y})^2 }}
$
Tiene las siguientes propiedades
-1 a menos o igual que 1.
Si el coeficiente de correlación se acerca a 1, \(x\) aumenta → \(y\) también aumenta
El valor del coeficiente de correlación no cambia cuando \(x, y\) se multiplican por un número bajo
Calcular el coeficiente de correlación entre dos columnas numéricas #
import numpy as np
np.random.seed(777) # para fijar números aleatorios
import matplotlib.pyplot as plt
import numpy as np
x = [xi + np.random.rand() for xi in np.linspace(0, 100, 40)]
y = [yi + np.random.rand() for yi in np.linspace(1, 50, 40)]
plt.figure(figsize=(5, 5))
plt.scatter(x, y)
plt.show()
coef = np.corrcoef(x, y)
print(coef)
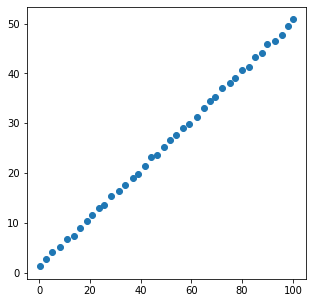
[[1. 0.99979848]
[0.99979848 1. ]]
Calcular colectivamente el coeficiente de correlación entre múltiples variables #
import seaborn as sns
df = sns.load_dataset("iris")
df.head()
Comprobar las COEFICIENCIAS DE CORRELACIÓN entre todas las variables #
Utilizando el conjunto de datos del iris, veamos la correlación entre las variables.
df.corr().style.background_gradient(cmap="YlOrRd")
En el mapa de calor, es difícil ver dónde es mayor la correlación. Compruebe el gráfico de barras para ver qué variables tienen la mayor correlación con longitud_de_sepal.
df.corr()["sepal_length"].plot.bar(grid=True, ylabel="corr")
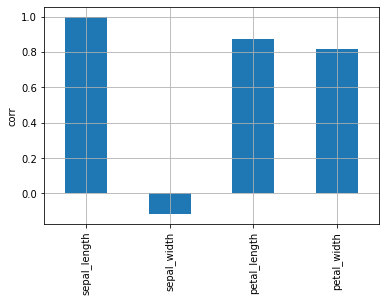
Cuando el coeficiente de correlación es bajo #
Compruebe la distribución de los datos cuando el coeficiente de correlación es bajo y confirme que el coeficiente de correlación puede ser bajo incluso cuando existe una relación entre las variables.
n_samples = 1000
plt.figure(figsize=(12, 12))
for i, ci in enumerate(np.linspace(-1, 1, 16)):
ci = np.round(ci, 4)
mean = np.array([0, 0])
cov = np.array([[1, ci], [ci, 1]])
v1, v2 = np.random.multivariate_normal(mean, cov, size=n_samples).T
plt.subplot(4, 4, i + 1)
plt.plot(v1, v2, "x")
plt.title(f"r={ci}")
plt.tight_layout()
plt.show()
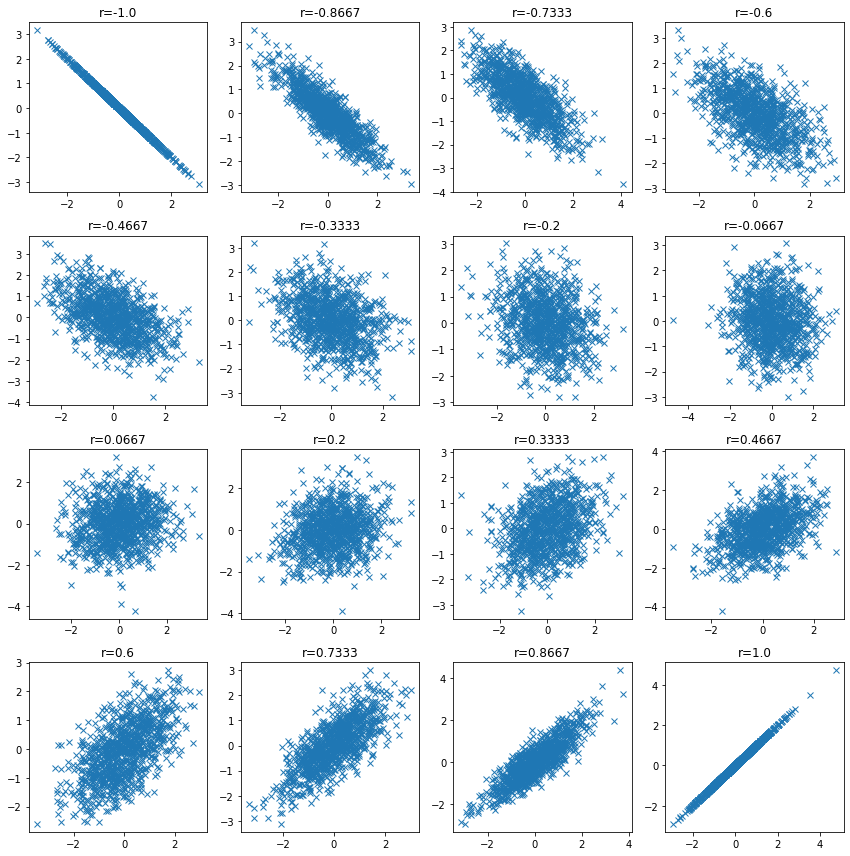
En algunos casos, existe una relación entre las variables aunque el coeficiente de correlación sea bajo.
Intentaremos crear un ejemplo de este tipo, aunque sea sencillo.
import japanize_matplotlib
from sklearn import datasets
japanize_matplotlib.japanize()
n_samples = 1000
circle, _ = datasets.make_circles(n_samples=n_samples, factor=0.1, noise=0.05)
moon, _ = datasets.make_moons(n_samples=n_samples, noise=0.05)
corr_circle = np.round(np.corrcoef(circle[:, 0], circle[:, 1])[1, 0], 4)
plt.title(f"correlation coefficient={corr_circle}", fontsize=23)
plt.scatter(circle[:, 0], circle[:, 1])
plt.show()
corr_moon = np.round(np.corrcoef(moon[:, 0], moon[:, 1])[1, 0], 4)
plt.title(f"correlation coefficient={corr_moon}", fontsize=23)
plt.scatter(moon[:, 0], moon[:, 1])
plt.show()

