Coeficiente de Determinación

4.2.2

Coeficiente de Determinación

Actualizado 2020-02-12 Lectura 4 min

Resumen

Coeficiente de Determinaciónの概要を押さえ、評価対象と読み取り方を整理します。
Python 3.13 のコード例で算出・可視化し、手順と実務での確認ポイントを確認します。
図表や補助指標を組み合わせ、モデル比較や閾値調整に活かすヒントをまとめます。

El coeficiente de determinación (en inglés: coefficient of determination, R2) es una métrica estadística que mide qué tan bien las variables independientes (variables explicativas) explican la variabilidad de la variable dependiente (variable objetivo). También se le conoce como tasa de contribución. Fuente:

Coeficiente de Determinación - Wikipedia

Generalmente, cuanto más alto sea, mejor es como métrica de evaluación.
En el mejor de los casos, toma el valor de 1.
Sin embargo, tiende a aumentar a medida que se añaden más características.
No se puede determinar la “alta precisión” del modelo basándose únicamente en esta métrica.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
import numpy as np

import matplotlib.pyplot as plt

import japanize_matplotlib

from sklearn.datasets import make_regression

from sklearn.ensemble import RandomForestRegressor

from sklearn.model_selection import train_test_split

python

Crear un modelo con datos de muestra y calcular el coeficiente de determinación #

Generar datos que sean fáciles de predecir #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

python

Calcular el Coeficiente de Determinación #

sklearn.metrics.roc_auc_score

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
from sklearn.metrics import r2_score

r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

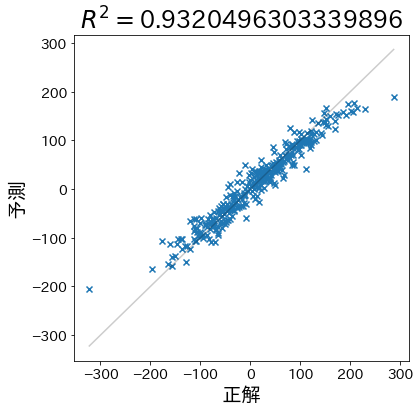
plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Valores Reales")

plt.ylabel("Predicciones")

Text(0, 0.5, '予測')

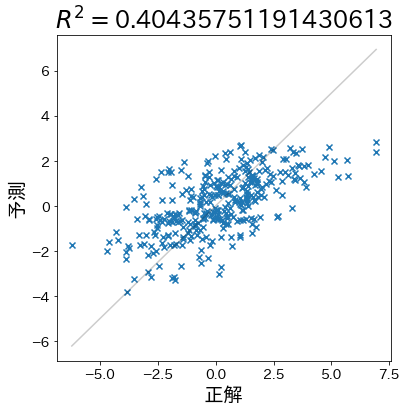
5, ‘予測’) (figura)

Generar datos difíciles de predecir #

Crearemos un conjunto de datos donde la relación entre las variables independientes y la variable dependiente sea más débil. Esto debería resultar en un coeficiente de determinación (R²) más bajo, reflejando una menor capacidad predictiva del modelo.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

model = RandomForestRegressor(max_depth=5)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Valores Reales")

plt.ylabel("Predicciones")

Text(0, 0.5, '予測')

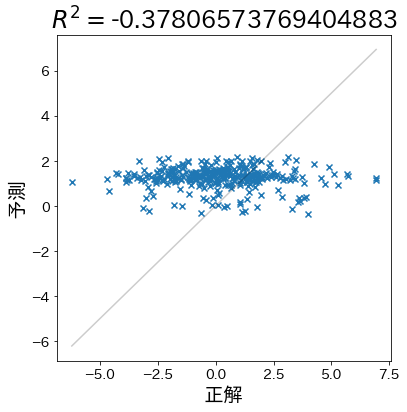
5, ‘予測’) (figura)

Cuando las predicciones son completamente aleatorias #

Si las predicciones son peores que simplemente predecir el promedio de los valores reales, el coeficiente de determinación (R²) puede tomar valores negativos. Esto indica que el modelo no es útil para capturar la relación entre las variables.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
X, y = make_regression(

    n_samples=1000,

    n_informative=3,

    n_features=20,

    effective_rank=4,

    noise=1.5,

    random_state=RND,

)

train_X, test_X, train_y, test_y = train_test_split(

    X, y, test_size=0.33, random_state=RND

)

# Reorganizar aleatoriamente train_y y transformar sus valores

train_y = np.random.permutation(train_y)

train_y = np.sin(train_y) * 10 + 1

model = RandomForestRegressor(max_depth=1)

model.fit(train_X, train_y)

pred_y = model.predict(test_X)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
r2 = r2_score(test_y, pred_y)

y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))

plt.title(f"$R^2 =${r2}")

plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", c="k", alpha=0.2)

plt.scatter(test_y, pred_y, marker="x")

plt.xlabel("Valores Reales")

plt.ylabel("Predicciones")

Text(0, 0.5, '予測')

5, ‘予測’) (figura)

Coeficiente de Determinación usando el Método de Mínimos Cuadrados #

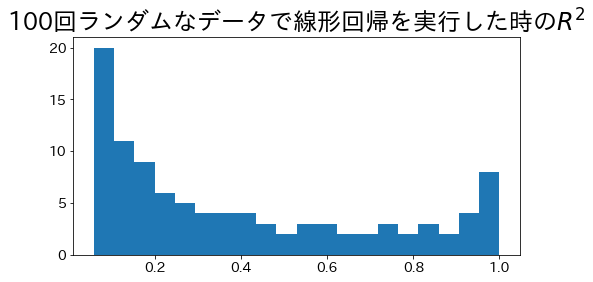
En una regresión lineal simple utilizando el método de mínimos cuadrados, el coeficiente de determinación (R²) siempre se encuentra en el rango de \(0 \le R^2 \le 1\).

Vamos a añadir ruido aleatorio a los datos y ejecutar la regresión lineal 100 veces para calcular y analizar los valores del coeficiente de determinación.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
from sklearn.linear_model import LinearRegression

from sklearn.pipeline import make_pipeline

from sklearn.preprocessing import StandardScaler

from sklearn.model_selection import train_test_split

from sklearn.metrics import r2_score

from sklearn.datasets import make_regression

import matplotlib.pyplot as plt

# Configuración inicial

RND = 42  # Semilla para reproducibilidad

r2_scores = []

for i in range(100):

    # Crear datos con ruido incremental

    X, y = make_regression(

        n_samples=500,

        n_informative=1,

        n_features=1,

        effective_rank=4,

        noise=i * 0.1,

        random_state=RND,

    )

    train_X, test_X, train_y, test_y = train_test_split(

        X, y, test_size=0.33, random_state=RND

    )

    # Modelo de regresión lineal

    model = make_pipeline(

        StandardScaler(with_mean=False), LinearRegression(positive=True)

    ).fit(train_X, train_y)

    # Calcular el coeficiente de determinación

    pred_y = model.predict(test_X)

    r2 = r2_score(test_y, pred_y)

    r2_scores.append(r2)

# Visualizar la distribución de los valores R²

plt.figure(figsize=(8, 4))

plt.title("Distribución de $R^2$ en 100 regresiones lineales con datos aleatorios")

plt.hist(r2_scores, bins=20)

plt.xlabel("$R^2$")

plt.ylabel("Frecuencia")

plt.show()

Vamos a añadir ruido aleatorio a los datos y ejecutar la reg… (figura)