Transformación Yeo-Johnson

Definición #

Para una observación (y) y un parámetro de potencia (\lambda), la transformación Yeo-Johnson (T_\lambda(y)) se define por tramos:

$$ T_\lambda(y)= \begin{cases} \dfrac{(y + 1)^\lambda - 1}{\lambda}, & y \ge 0,\ \lambda \ne 0,\\ \log(y + 1), & y \ge 0,\ \lambda = 0,\\ -\dfrac{(1 - y)^{2 - \lambda} - 1}{2 - \lambda}, & y < 0,\ \lambda \ne 2,\\ -\log(1 - y), & y < 0,\ \lambda = 2. \end{cases} $$

• Con (\lambda = 1) se recupera el valor original.
• Para (y \ge 0) el comportamiento coincide con una transformación Box-Cox sobre (y + 1).
• Los valores negativos se reflejan alrededor de cero, por lo que la transformación sigue siendo monótona incluso cuando cambia el signo.
• La trasformación inversa se obtiene resolviendo cada caso para (y); SciPy la ofrece en scipy.stats.yeojohnson_inverse.

Normalmente (\lambda) se estima maximizando la verosimilitud bajo el supuesto de normalidad después de transformar los datos. SciPy implementa este estimador mediante yeojohnson_normmax.

Ejemplo práctico #

from scipy import stats
import matplotlib.pyplot as plt

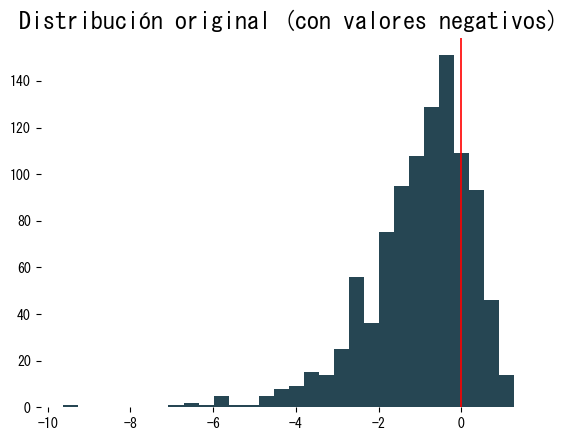
x = stats.loggamma.rvs(1, size=1_000) - 0.5
plt.hist(x, bins=30)
plt.axvline(x=0, color="r")
plt.title("Distribución original (con valores negativos)")
plt.show()

from scipy.stats import yeojohnson, yeojohnson_normmax

lmbda = yeojohnson_normmax(x)  # estimación de máxima verosimilitud
print(f"λ estimado: {lmbda:.3f}")

x_trans = yeojohnson(x, lmbda=lmbda)
plt.hist(x_trans, bins=30)
plt.title("Después de Yeo-Johnson")
plt.show()

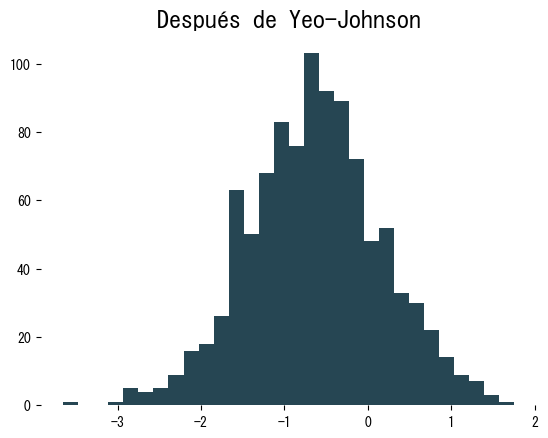
Tras la transformación la distribución es mucho más simétrica. Debido a que fijamos (\lambda), podemos reutilizar el mismo valor en otros subconjuntos del conjunto de datos:

X_train_trans = yeojohnson(X_train, lmbda=lmbda)
X_valid_trans = yeojohnson(X_valid, lmbda=lmbda)  # reutilizar λ

Consejos prácticos #

• Si el modelo espera variables centradas y escaladas, normaliza después de aplicar Yeo-Johnson (StandardScaler, por ejemplo).
• Calcula (\lambda) únicamente con el conjunto de entrenamiento y reutilízalo en validación o prueba para evitar fugas de información.
• Cuando aún existan colas pesadas, combina la transformación con escalados robustos (RobustScaler) para mitigar el impacto de los outliers.

La transformación Yeo-Johnson es un sustituto directo de Box-Cox en pipelines de preprocesamiento que no pueden asumir datos estrictamente positivos.