5.14.1
Profeta
Meta (Facebook) ha publicado una biblioteca de código abierto (OSS) para la predicción de series temporales. Puedes consultar las instrucciones de instalación en Python en Installation in Python. Básicamente, solo necesitas ejecutar pip install prophet para instalarla.
Taylor, Sean J., y Benjamin Letham. “Forecasting at scale.” The American Statistician 72.1 (2018): 37-45.
| |
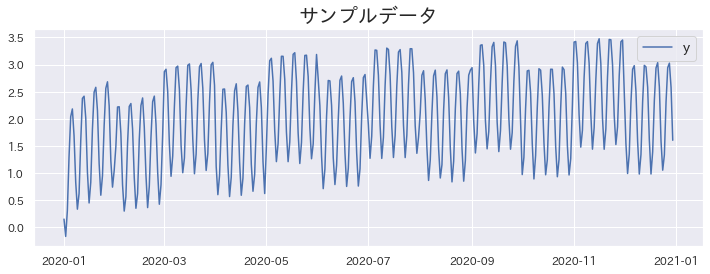
Datos utilizados para el experimento #
Se utilizarán datos de un año. Los meses pares tienden a mostrar una disminución en los valores. Además, los datos presentan un comportamiento cíclico semanalmente.
El período abarca desde el 01/01/2020 hasta el 31/12/2020.
| |
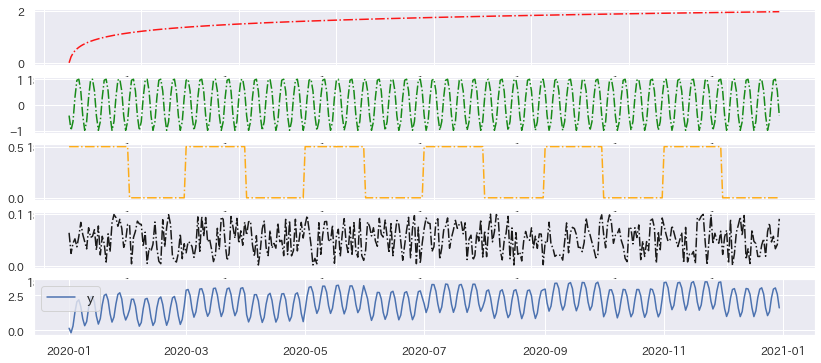
Componentes de los datos de series temporales #
El término “datos de series temporales” incluye diferentes tipos de datos. Aquí nos centraremos en los siguientes casos:
- Los datos contienen solo marcas de tiempo y valores numéricos.
- Las marcas de tiempo no tienen valores faltantes y están espaciadas de manera uniforme (evenly spaced).
Visualización de los componentes de los datos #
| |
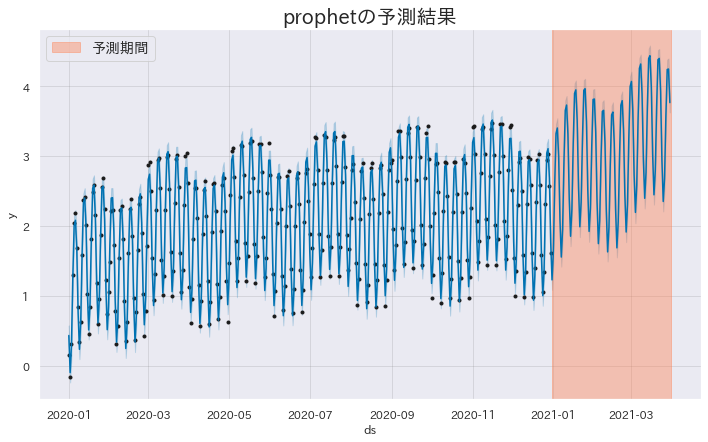
Predicción con Prophet para el período de enero a marzo de 2021 #
Utilizaremos los datos desde el 1 de enero de 2020 hasta el 31 de diciembre de 2020 para predecir los próximos tres meses (enero a marzo de 2021). Dado que solo contamos con un año de datos, desactivaremos la estacionalidad anual (yearly_seasonality=False). Sin embargo, dado que se observa periodicidad semanal, habilitaremos la estacionalidad diaria (daily_seasonality=True).
Código para entrenar y predecir con Prophet #
| |
| |
Initial log joint probability = -32.1541
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
99 772.276 5.98161e-05 56.7832 1 1 135
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
131 772.59 0.00128893 157.592 1.465e-05 0.001 217 LS failed, Hessian reset
181 772.678 3.78737e-05 49.0389 6.852e-07 0.001 326 LS failed, Hessian reset
199 772.681 1.42622e-06 43.2231 0.6929 0.6929 350
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
230 772.681 6.80165e-06 56.0478 7.185e-08 0.001 432 LS failed, Hessian reset
245 772.681 4.06967e-08 48.5475 0.1802 0.8285 454
Optimization terminated normally:
Convergence detected: relative gradient magnitude is below tolerance
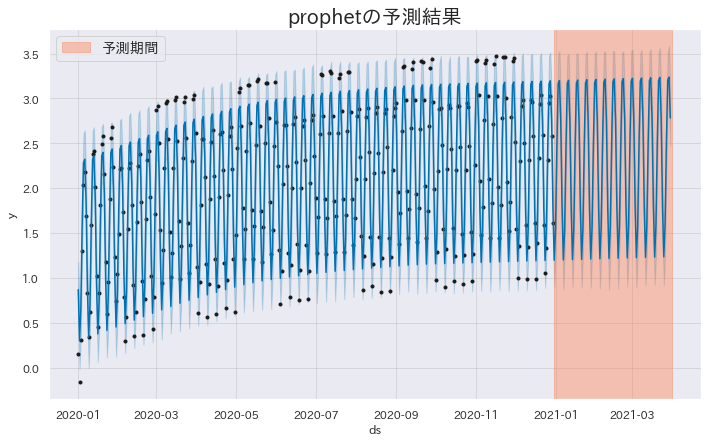
Impacto de la especificación de periodicidad #
En el siguiente ejemplo, se fuerza la especificación de estacionalidad anual (yearly_seasonality=True). Como resultado, debido al término añadido para capturar ciclos anuales, se observa un aumento algo inusual en las predicciones para 2022.
| |
Initial log joint probability = -32.1541
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
99 1076.54 0.000445309 68.8033 1 1 133
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
199 1078.13 0.000151685 92.7241 1 1 256
Iter log prob ||dx|| ||grad|| alpha alpha0 # evals Notes
246 1078.14 1.78997e-06 84.0649 1.52e-08 0.001 353 LS failed, Hessian reset
261 1078.14 3.82403e-08 101.692 0.2973 1 372
Optimization terminated normally:
Convergence detected: relative gradient magnitude is below tolerance