Comprobar el conjunto de datos

Vea lo que hay en los datos #

import datetime
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

from scipy import stats
from statsmodels.tsa import stattools

Lectura de un conjunto de datos desde un archivo csv #

data = pd.read_csv("sample.csv")
data.head(10)

	Date	Temp
0	1981-01-01	20.7
1	1981-01-02	17.9
2	1981-01-03	18.8
3	1981-01-04	14.6
4	1981-01-05	15.8
5	1981-01-06	15.8
6	1981-01-07	15.8
7	1981-01-08	17.4
8	1981-01-09	21.8
9	1981-01-10	20.0

Establecer la marca de tiempo en datetime #

La columna Fecha se lee actualmente como un tipo de objeto, es decir, una cadena. Para tratarla como una marca de tiempo, utilice lo siguiente datetime — Basic Date and Time Types para convertirla en un tipo datetime.

data["Date"] = data["Date"].apply(
    lambda x: datetime.datetime.strptime(str(x), "%Y-%m-%d")
)

print(f"Date column dtype: {data['Date'].dtype}")

Date column dtype: datetime64[ns]

Obtener una visión general de una serie temporal #

pandas.DataFrame.describe #

Para empezar, revisamos brevemente el aspecto de los datos. Utilizaremos pandas.DataFrame.describe para comprobar algunas estadísticas simples para la columna Temp.

data.describe()

	Temp
count	3650.000000
mean	11.177753
std	4.071837
min	0.000000
25%	8.300000
50%	11.000000
75%	14.000000
max	26.300000

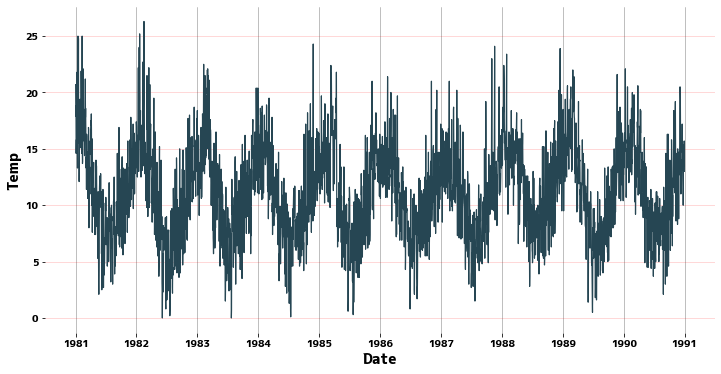
Gráfico de líneas #

Utilice seaborn.lineplot para ver el aspecto del ciclo.

plt.figure(figsize=(12, 6))
sns.lineplot(x=data["Date"], y=data["Temp"])
plt.ylabel("Temp")
plt.grid(axis="x")
plt.grid(axis="y", color="r", alpha=0.3)
plt.show()

png

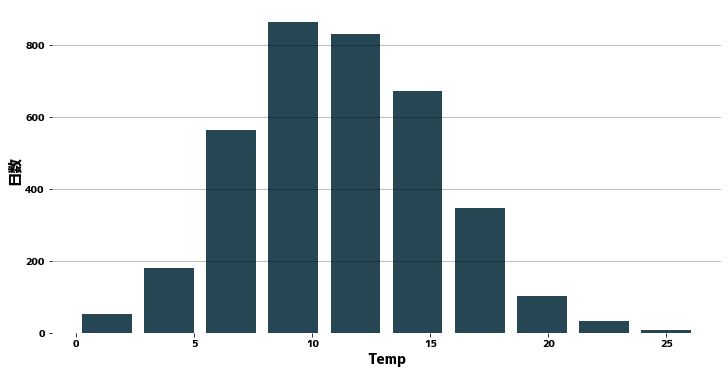
Histogram #

plt.figure(figsize=(12, 6))
plt.hist(x=data["Temp"], rwidth=0.8)
plt.xlabel("Temp")
plt.ylabel("日数")
plt.grid(axis="y")
plt.show()

png

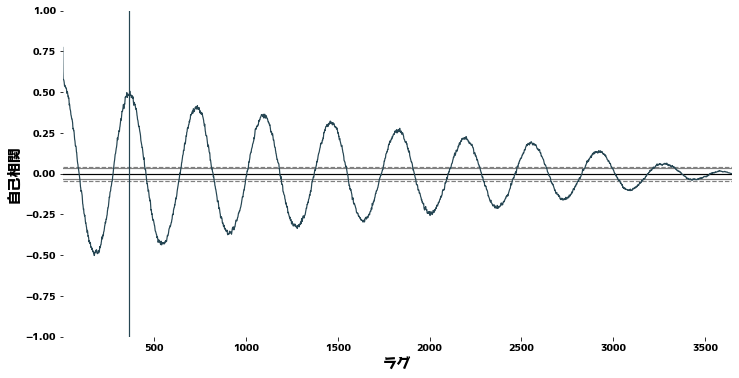
Autocorrelación y colerogramas #

Usando pandas.plotting.autocorrelation_plot Comprueba la autocorrelación para verificar la periodicidad de los datos de las series temporales. A grandes rasgos, la autocorrelación es una medida de lo bien que una señal coincide con una señal desplazada en el tiempo de sí misma, expresada en función de la magnitud del desplazamiento temporal.

plt.figure(figsize=(12, 6))
pd.plotting.autocorrelation_plot(data["Temp"])
plt.grid()
plt.axvline(x=365)
plt.xlabel("lag")
plt.ylabel("autocorrelation")
plt.show()

png

Prueba de raíz unitaria #

Comprobamos si los datos presentan un proceso de raíz unitaria. La prueba Dickey-Fuller aumentada se utiliza para comprobar la hipótesis nula de un proceso de raíz unitaria.

statsmodels.tsa.stattools.adfuller

stattools.adfuller(data["Temp"], autolag="AIC")

(-4.444804924611697,
 0.00024708263003610177,
 20,
 3629,
 {'1%': -3.4321532327220154,
  '5%': -2.862336767636517,
  '10%': -2.56719413172842},
 16642.822304301197)

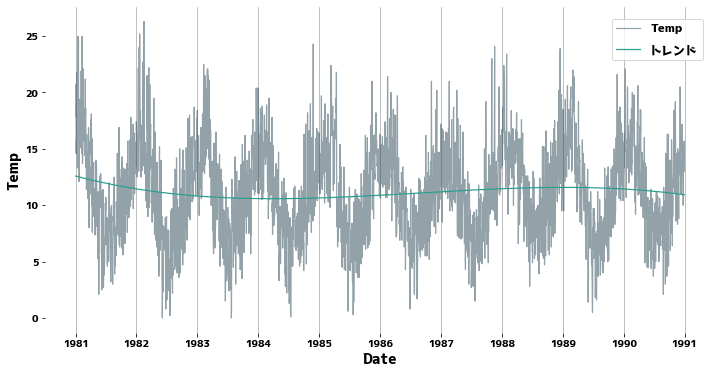
Comprobación de la tendencia #

La línea de tendencia se dibuja ajustando un polinomio unidimensional a la serie temporal. Dado que los datos en este caso son casi estacionarios, casi no hay tendencia.

numpy.poly1d — NumPy v1.22 Manual

def get_trend(timeseries, deg=3):
    """Crear una línea de tendencia para datos de series temporales

    Args:
        timeseries(pd.Series) : datos de series temporales

    Returns:
        pd.Series: línea de tendencia
    """
    x = list(range(len(timeseries)))
    y = timeseries.values
    coef = np.polyfit(x, y, deg)
    trend = np.poly1d(coef)(x)
    return pd.Series(data=trend, index=timeseries.index)

data["Trend"] = get_trend(data["Temp"])

plt.figure(figsize=(12, 6))
sns.lineplot(x=data["Date"], y=data["Temp"], alpha=0.5, label="Temp")
sns.lineplot(x=data["Date"], y=data["Trend"], label="トレンド")
plt.grid(axis="x")
plt.legend()
plt.show()

png

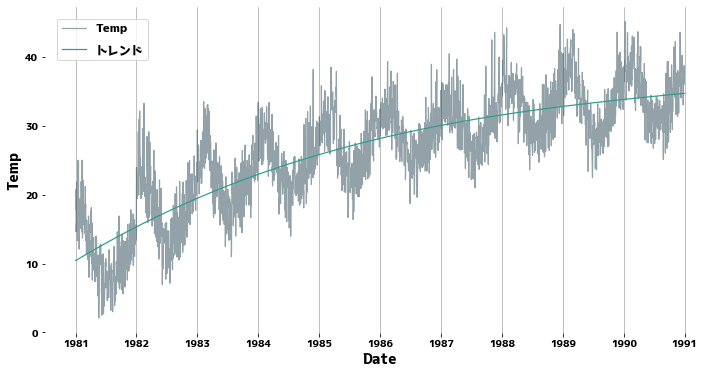
Suplemento: Si hay una tendencia clara #

La línea verde es la línea de tendencia.

data_sub = data.copy()
data_sub["Temp"] = (
    data_sub["Temp"] + np.log(data_sub["Date"].dt.year - 1980) * 10
)  # Dummy Trends
data_sub["Trend"] = get_trend(data_sub["Temp"])

plt.figure(figsize=(12, 6))
sns.lineplot(x=data_sub["Date"], y=data_sub["Temp"], alpha=0.5, label="Temp")
sns.lineplot(x=data_sub["Date"], y=data_sub["Trend"], label="トレンド")
plt.grid(axis="x")
plt.legend()
plt.show()

png