Dynamic Time Warping (DTW)

Actualizado 2020-01-29 Lectura 4 min

Resumen

DTW alinea dos series temporales permitiendo estiramientos locales del eje temporal para minimizar la distancia acumulada.
El algoritmo construye una matriz de distancias, calcula costos acumulados mediante programación dinámica y recupera la trayectoria de alineación óptima.
Implementamos DTW con NumPy, lo comparamos con fastdtw y visualizamos el camino de warping resultante.

¿Qué es DTW? #

Dynamic Time Warping mide la similitud entre dos secuencias cuya velocidad o fase inicial puede variar. Encuentra la trayectoria con el menor costo acumulado para alinear ambas secuencias. Se utiliza en reconocimiento de voz, análisis de sensores, y sistemas de recomendación que comparan patrones temporales de uso.

DTW con NumPy #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np

def dtw_distance(
    x: np.ndarray,
    y: np.ndarray,
    window: int | None = None,
) -> tuple[float, list[tuple[int, int]]]:
    n, m = len(x), len(y)
    window = max(window or max(n, m), abs(n - m))

    cost = np.full((n + 1, m + 1), np.inf)
    cost[0, 0] = 0.0

    for i in range(1, n + 1):
        for j in range(max(1, i - window), min(m + 1, i + window + 1)):
            dist = abs(x[i - 1] - y[j - 1])
            cost[i, j] = dist + min(cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1])

    i, j = n, m
    path: list[tuple[int, int]] = []
    while i > 0 and j > 0:
        path.append((i - 1, j - 1))
        idx = np.argmin((cost[i - 1, j], cost[i, j - 1], cost[i - 1, j - 1]))
        if idx == 0:
            i -= 1
        elif idx == 1:
            j -= 1
        else:
            i -= 1
            j -= 1

    path.reverse()
    return cost[n, m], path

Comparar tres series #

1
2
python --version  # ej.: Python 3.13.0
pip install matplotlib fastdtw

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
import matplotlib.pyplot as plt
from fastdtw import fastdtw

np.random.seed(42)
t = np.arange(0, 30)

series_a = 1.2 * np.sin(t / 2.0)
series_b = 1.1 * np.sin((t + 2) / 2.1) + 0.05 * np.random.randn(len(t))
series_c = 0.8 * np.cos(t / 2.0) + 0.05 * np.random.randn(len(t))

plt.figure(figsize=(10, 3))
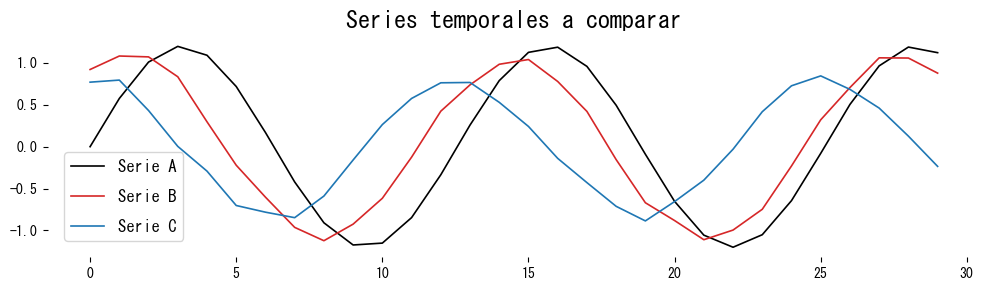
plt.plot(t, series_a, label="Serie A", color="black")
plt.plot(t, series_b, label="Serie B", color="tab:red")
plt.plot(t, series_c, label="Serie C", color="tab:blue")
plt.title("Series temporales a comparar")
plt.legend()
plt.tight_layout()
plt.show()

Comparar tres series (figura)

1
2
3
4
5
6
7
8
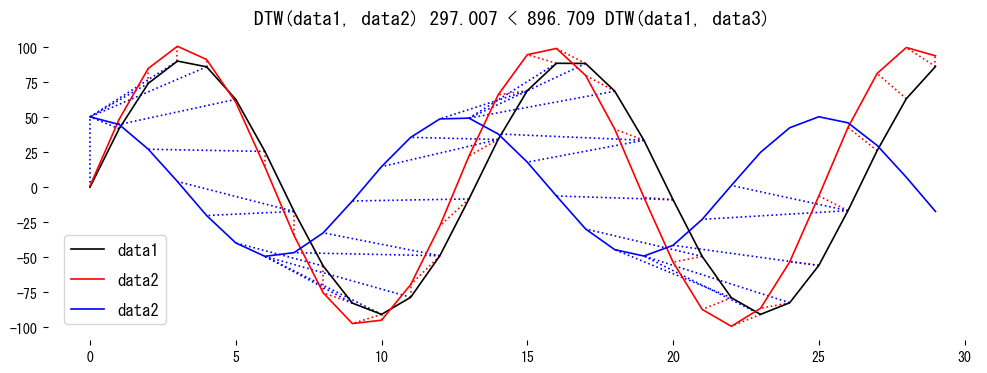
dist_ab, path_ab = dtw_distance(series_a, series_b)
dist_ac, path_ac = dtw_distance(series_a, series_c)

fast_dist_ab, _ = fastdtw(series_a, series_b)
fast_dist_ac, _ = fastdtw(series_a, series_c)

print(f"DTW(A, B)  = {dist_ab:.3f}  / fastdtw = {fast_dist_ab:.3f}")
print(f"DTW(A, C)  = {dist_ac:.3f}  / fastdtw = {fast_dist_ac:.3f}")

La Serie B mantiene una forma similar a la Serie A, por lo que ambas distancias son pequeñas. La Serie C difiere en su forma y genera una distancia mayor.

Visualizar la trayectoria de warping #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
def plot_warping(a: np.ndarray, b: np.ndarray, path: list[tuple[int, int]]) -> None:
    fig, axes = plt.subplots(
        1,
        2,
        figsize=(12, 4),
        gridspec_kw={"width_ratios": [1, 1.2]},
    )

    axes[0].plot(a, label="Serie A", color="black")
    axes[0].plot(b, label="Serie B", color="tab:red")
    axes[0].set_title("Series temporales")
    axes[0].legend()

    axes[1].imshow(
        np.abs(np.subtract.outer(a, b)),
        origin="lower",
        interpolation="nearest",
        cmap="viridis",
    )
    path_arr = np.array(path)
    axes[1].plot(path_arr[:, 1], path_arr[:, 0], color="white", linewidth=2)
    axes[1].set_title("Costo acumulado y trayectoria")
    axes[1].set_xlabel("Índice Serie B")
    axes[1].set_ylabel("Índice Serie A")
    plt.tight_layout()
    plt.show()

plot_warping(series_a, series_b, path_ab)

Visualizar la trayectoria de warping (figura)

El camino blanco muestra cómo DTW estira o comprime las series para alinear picos y valles aun cuando ocurren en tiempos distintos.

Conclusiones #

DTW alinea secuencias con tempo variable minimizando el costo acumulado de una trayectoria de warping.
La programación dinámica ofrece el camino óptimo; restricciones de ventana o fastdtw ayudan a acelerar el cálculo.
Con NumPy basta para una implementación básica, y la visualización facilita entender el comportamiento del algoritmo.