MCC

中級

4.3.5

MCC

最終更新 2020-03-25 読了時間 2 分
まとめ
  • Matthews 相関係数は二値分類の予測と真値の相関を測る指標です。
  • 混同行列から MCC を計算し、極端な不均衡でも安定する特性を確認します。
  • モデル比較で MCC を使うときの注意点や閾値の扱いを整理します。
  • 混同行列 の概念を先に学ぶと理解がスムーズです

1. 定義 #

二値分類において MCC は次式で表されます。

$$ \mathrm{MCC} = \frac{TP \cdot TN - FP \cdot FN}{\sqrt{(TP + FP)(TP + FN)(TN + FP)(TN + FN)}} $$
  • 1 … 完全に正しい分類
  • 0 … ランダム予測と同程度
  • −1 … 完全に逆の予測 多クラスでも同様に、クラスごとの混同行列から拡張できます。

2. Python 3.13 での計算 #

1
2

python --version        # 例: Python 3.13.0
pip install scikit-learn matplotlib

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

from sklearn.datasets import make_classification
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import matthews_corrcoef, confusion_matrix
from sklearn.model_selection import train_test_split
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
X, y = make_classification(
    n_samples=40_000,
    n_features=20,
    n_informative=6,
    weights=[0.95, 0.05],
    random_state=42,
)
X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.25, stratify=y, random_state=42
)
model = make_pipeline(
    StandardScaler(),
    LogisticRegression(max_iter=2000, class_weight="balanced"),
)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
print(confusion_matrix(y_test, y_pred))
print("MCC:", matthews_corrcoef(y_test, y_pred))

class_weight=“balanced” を指定すると少数クラスの影響も MCC に反映しやすくなります。

3. 閾値と MCC の関係 #

確率出力から MCC を閾値ごとに算出すると、バランスの良いポイントがわかります。

MCC と閾値

閾値ごとの MCC。クラス不均衡でも、最大値付近の閾値を使えば相関が高まりやすい。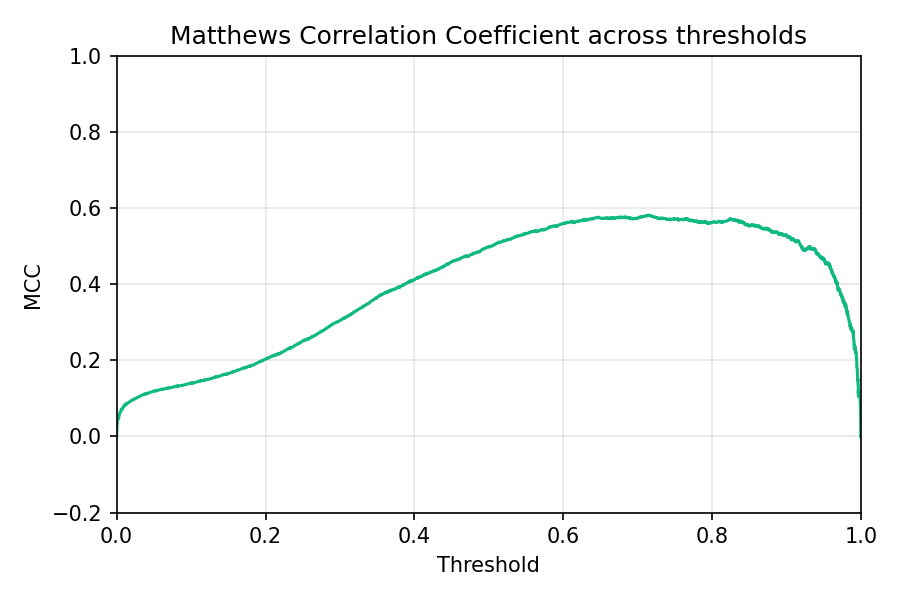

F1 スコアと異なり TN も評価に含まれるため、クラス比率が極端でも安定して比較できます。

4. 実務での活用 #

  • Accuracy の補助 – Accuracy が高くても MCC が低い場合、どちらかのクラスが無視されている可能性があります。
  • モデル比較 – Grid Search のスコアリングとして make_scorer(matthews_corrcoef) を指定すれば MCC を最適化できます。
  • 閾値チューニング – ROC や PR 曲線と併用し、MCC が最大になる閾値を候補にすると全体バランスが把握しやすいです。

まとめ #

  • MCC は TP/FP/FN/TN を同時に考慮する相関指標で、−1〜1 のスケールでわかりやすく評価できる。
  • Python 3.13 では matthews_corrcoef で簡単に算出でき、閾値別に可視化すると最適な動作点が見える。
  • Accuracy や F1 と併用して、クラス不均衡下でも偏りのない評価を行おう。

閾値と各指標 #

閾値を動かして各指標の変化を確認してください。