Kullback-Leibler ダイバージェンス

中級

4.4.1

Kullback-Leibler ダイバージェンス

最終更新 2020-03-11 読了時間 2 分
まとめ
  • KL ダイバージェンスは「基準分布に対してどれだけ情報量が増えるか」を測る指標です。
  • 離散分布の例で計算手順とゼロ確率に対するスムージング方法を確認します。
  • 生成モデル評価やモニタリングで活用する際の注意点を整理します。

1. KL ダイバージェンスとは #

KL ダイバージェンスは、基準分布 \(Q\) を想定したときに実際の分布 \(P\) がどれだけ異なるかを相対エントロピーとして表します。

$$ \mathrm{KL}(P \parallel Q) = \sum_i p_i \log \frac{p_i}{q_i} $$
  • \(\mathrm{KL}(P \parallel Q) = 0\) のとき、分布は一致します。
  • 非対称性を持ち、一般に \(\mathrm{KL}(P \parallel Q) \neq \mathrm{KL}(Q \parallel P)\) です。
  • \(q_i = 0\) かつ \(p_i > 0\) の場合は無限大となるため、サポートの違いに敏感です。

2. Python での基本実装 #

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import numpy as np
from scipy.special import rel_entr  # 元素ごとの p * log(p / q)

def kl_divergence(p: np.ndarray, q: np.ndarray) -> float:
    """KL ダイバージェンス D(P || Q) を計算する。"""
    p = np.asarray(p, dtype=float)
    q = np.asarray(q, dtype=float)

    p = p / p.sum()
    q = q / q.sum()

    epsilon = 1e-12
    return float(np.sum(rel_entr(p + epsilon, q + epsilon)))

rel_entr を用いると、配列要素ごとの \(p_i \log \frac{p_i}{q_i}\) を安全に計算できます。ゼロ確率が含まれる場合は微小値 \(\epsilon\) を加えるなどのスムージングを事前に行いましょう。

3. ヒストグラム例での比較 #

以下は 2 つの離散分布（棒グラフ）を比較した例です。

1
2
3
4
5
6
7
8
9

import matplotlib.pyplot as plt
a = np.array([0.1, 0.2, 0.3, 0.2, 0.1, 0.1])
b = np.array([0.05, 0.1, 0.2, 0.3, 0.3, 0.05])

plt.figure(figsize=(12, 4))
plt.bar(np.arange(a.size) - 0.1, a, width=0.2, label="p")
plt.bar(np.arange(b.size) + 0.1, b, width=0.2, label="q")
plt.legend()
plt.show()
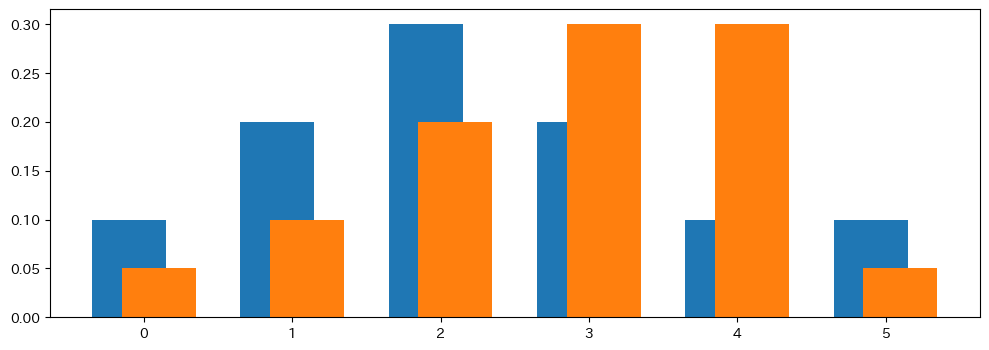
2つの離散分布の比較

分布pとqを棒グラフで並べた例。形状の違いがKLダイバージェンスの大きさに反映される。

同じ観測値から得られた分布を比較すると、KL は 0 になります。

1
2
3

print(f"KL(p || p) = {kl_divergence(a, a):.4f}")
print(f"KL(p || b) = {kl_divergence(a, b):.4f}")
print(f"KL(b || a) = {kl_divergence(b, a):.4f}")

結果が示すように、順序を入れ替えると値が変わるため、どちらを基準とするかで解釈が異なります。

4. Jensen–Shannon ダイバージェンスへの接続 #

KL の非対称性を解消したい場合は、両方向の KL を平均した Jensen–Shannon ダイバージェンスを用います。以下の図は 2 つの正規分布とその平均分布のイメージです。

1
2
3
4

plt.hist(np.random.normal(1, 1, 1000), alpha=0.85, color="blue")
plt.hist(np.random.normal(4, 1, 1000), alpha=0.85, color="red")
plt.hist(np.random.normal(2.5, 1, 1000), alpha=0.85, color="green")
plt.show()
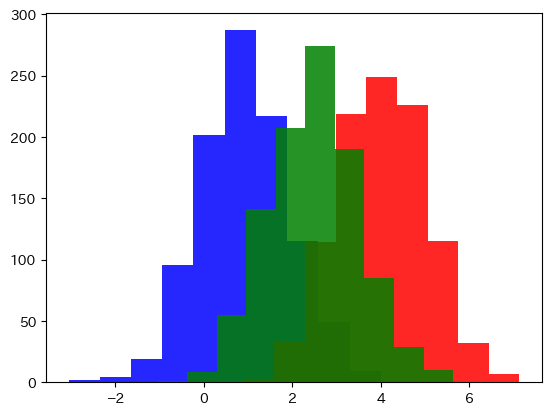
2つの正規分布とその平均分布

青と赤の正規分布の中間（緑）を基準にすると、Jensen-Shannonダイバージェンスが計算できる。

5. 実務での活用例と注意点 #

  • 生成モデル評価：生成分布が教師データから離れていないかをチェック。
  • 監視・ドリフト検知：配信データが学習時分布からどれだけ乖離しているかをモニタリング。
  • 言語モデル：n-gram 分布や出力確率の差異を測定。

注意点として、サンプル数が少ない場合は推定が不安定になるため、ディリクレ事前分布によるスムージングなどを組み合わせます。また、距離が大きい場合でも必ずしも性能悪化を意味しないため、他の指標と合わせて解釈しましょう。

まとめ #

KL ダイバージェンスは「基準分布との相対的な情報量差」を表し、モデルの評価や監視で広く利用されます。非対称性やゼロ確率への感度といった性質を理解し、適切なスムージングと併せて活用してください。

分布の差と KL ダイバージェンス #

2 つの分布の差を変えると KL ダイバージェンスがどう変化するか確認できます。