まとめ
- Validation Curve はハイパーパラメータを変化させたときの学習スコアと検証スコアの関係を可視化する手法です。
validation_curveを使い、正則化係数を変えながらトレーニング・検証曲線を描画して最適な範囲を特定します。- ハイパーパラメータ探索や過学習判定に活用する際の読み方と注意点を整理します。
1. Validation Curve とは #
Validation Curve は、特定のハイパーパラメータを変化させたときに学習データと検証データで得られるスコアを並べたものです。通常は次のように判断します。
- 学習スコアが高いが検証スコアが低い：モデルが過学習している可能性が高く、正則化を強める・木の深さを浅くするなどの調整が有効です。
- 両方のスコアが低い：モデルが十分に表現できておらず、正則化を弱める、より複雑なモデルに切り替えるなどの改善が必要です。
- 両スコアが近く高い：汎化性能が高い設定に近づいており、他の指標とあわせて最適なハイパーパラメータを判断します。
Learning Curve が「サンプル数とスコア」の関係を調べるのに対し、Validation Curve は「ハイパーパラメータとスコア」の関係を読み解くためのツールです。
2. Python 3.13 での例 #
以下のスクリプトでは、分類タスクに対してサポートベクタマシン（RBF カーネル）を適用し、正則化係数 \(C\) の値ごとに学習スコアと検証スコアを描画します。
from __future__ import annotations
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification
from sklearn.model_selection import validation_curve
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import SVC
def plot_validation_curve_for_svc() -> None:
"""SVC の正則化係数に対する検証曲線を描画して保存する。"""
features, labels = make_classification(
n_samples=1200,
n_features=20,
n_informative=5,
n_redundant=2,
n_repeated=0,
n_classes=2,
weights=[0.6, 0.4],
flip_y=0.02,
class_sep=1.2,
random_state=42,
)
model = make_pipeline(StandardScaler(), SVC(kernel="rbf", gamma="scale"))
param_range = np.logspace(-3, 2, 10)
train_scores, valid_scores = validation_curve(
estimator=model,
X=features,
y=labels,
param_name="svc__C",
param_range=param_range,
scoring="roc_auc",
cv=5,
n_jobs=None,
)
train_mean = train_scores.mean(axis=1)
train_std = train_scores.std(axis=1)
valid_mean = valid_scores.mean(axis=1)
valid_std = valid_scores.std(axis=1)
plt.figure(figsize=(7, 5))
plt.semilogx(param_range, train_mean, label="Train score", color="#1d4ed8")
plt.fill_between(
param_range,
train_mean - train_std,
train_mean + train_std,
alpha=0.2,
color="#1d4ed8",
)
plt.semilogx(param_range, valid_mean, label="Validation score", color="#ea580c")
plt.fill_between(
param_range,
valid_mean - valid_std,
valid_mean + valid_std,
alpha=0.2,
color="#ea580c",
)
plt.title("Validation Curve for SVC (ROC-AUC)")
plt.xlabel("Regularization parameter C")
plt.ylabel("Score")
plt.ylim(0.5, 1.05)
plt.legend(loc="best")
plt.grid(alpha=0.3)
plot_validation_curve_for_svc()
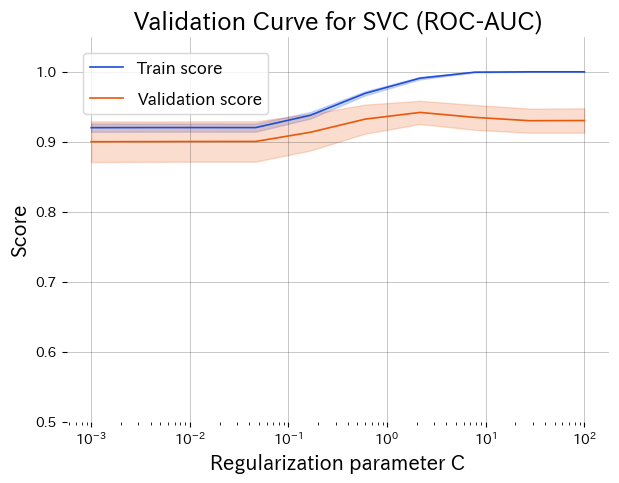
正則化係数 C を変化させたときの学習スコア（青）と検証スコア（橙）。検証スコアがピークになる付近が汎化性能の高い設定。
3. グラフの読み取りと意思決定 #
- 左端（小さな \(C\)）：強い正則化でモデルが単純化しすぎ、学習スコア・検証スコアともに低い（アンダーフィット）。
- 右端（大きな \(C\)）：正則化が弱まり、学習スコアだけが高止まりして検証スコアが低下（オーバーフィット）。
- 中央付近のピーク：学習スコアと検証スコアの差が小さく、検証スコアが最大になるパラメータ領域が最有力候補。
この例では \(C \approx 1\) 付近で検証スコアが最も高く、汎化性能と学習性能のバランスが取れていることが分かります。
4. 実務での活用と注意点 #
- 探索の事前調査：重要なハイパーパラメータを 1 つ選び、Validation Curve で有効なレンジを把握してからグリッドサーチやベイズ最適化に進むと効率的です。
- スコアのばらつきを確認：データ量が少ない場合は誤差が大きいため、平均値だけでなく標準偏差の帯域も併せて確認します。
- 複数パラメータの優先順位付け：主要パラメータごとに Validation Curve を作成し、探索の優先度や組み合わせの当たりを付けます。
- Learning Curve との併用：Validation Curve で「どのパラメータが効くか」を把握し、Learning Curve で「十分なサンプル数があるか」を確認すると改善方針が立てやすくなります。
Validation Curve を活用すると、ハイパーパラメータ調整の方向性が直感的に把握でき、チーム内での意思決定や説明にも役立ちます。モデルごとにこうした図を用意しておくと、改善施策の議論がスムーズになります。