決定係数

入門

4.2.2

決定係数

最終更新 2020-02-12 読了時間 3 分

まとめ

決定係数 \(R^2\) はモデルが目的変数の分散をどれだけ説明できたかを示す代表的な回帰指標です。
Python での算出例を通じて、高い値・低い値・負の値それぞれの解釈を確認します。
非線形モデルやサンプルが少ない場面での注意点、他指標との使い分けを整理します。

1. 定義と直感 #

決定係数 \(R^2\) は「ベースライン（平均予測）に比べてどれだけ誤差が減ったか」を測る指標です。

$$ R^2 = 1 - \frac{\sum_i (y_i - \hat{y}_i)^2}{\sum_i (y_i - \bar{y})^2} $$

\(R^2 = 1\)：誤差が 0（完全に当てている状態）。
\(R^2 = 0\)：平均だけを予測したのと同じ。
\(R^2 < 0\)：平均よりも誤差が大きく、モデルが悪化している。

特徴量を増やすと \(R^2\) は単調に大きくなるため、過学習の影響を受けやすい点に注意が必要です。

2. Python で計算する #

sklearn.metrics.r2_score を利用すると簡単に算出できます。ここでは説明変数 20 個・情報量 3 個を持つデータを生成し、ランダムフォレスト回帰で学習した例を示します。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_regression
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score
from sklearn.model_selection import train_test_split

RANDOM_STATE = 42

X, y = make_regression(
    n_samples=1_000,
    n_informative=3,
    n_features=20,
    noise=5.0,
    random_state=RANDOM_STATE,
)

train_X, test_X, train_y, test_y = train_test_split(
    X, y, test_size=0.33, random_state=RANDOM_STATE
)

model = RandomForestRegressor(max_depth=5, random_state=RANDOM_STATE)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)

r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", color="black", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x")
plt.xlabel("True")
plt.ylabel("Predicted")
plt.title(f"R^2 = {r2:.3f}")
plt.grid(alpha=0.3)
plt.show()

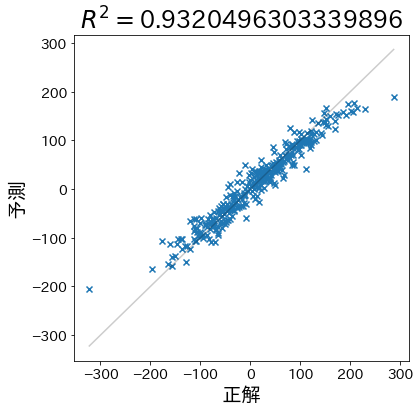
予測値と実測値の散布図（高R²） — 予測がほぼ対角線上に並び、R²が高い状態。ノイズが小さくモデルが分散をよく説明できている。

学習・検証データが同じ分布から生成されているため、予測はほぼ対角線上に並び、\(R^2\) も高くなります。

3. ばらつきが大きいデータと負の値 #

特徴量間に多くの相関があり、ノイズが大きい場合は \(R^2\) が低くなります。それでも平均予測よりは良い場合、0～1 の範囲に収まります。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
X, y = make_regression(
    n_samples=1_000,
    n_informative=3,
    n_features=20,
    effective_rank=4,
    noise=30.0,
    random_state=RANDOM_STATE,
)

train_X, test_X, train_y, test_y = train_test_split(
    X, y, test_size=0.33, random_state=RANDOM_STATE
)

model = RandomForestRegressor(max_depth=5, random_state=RANDOM_STATE)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)

r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", color="black", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x", alpha=0.6)
plt.xlabel("True")
plt.ylabel("Predicted")
plt.title(f"R^2 = {r2:.3f}")
plt.grid(alpha=0.3)
plt.show()

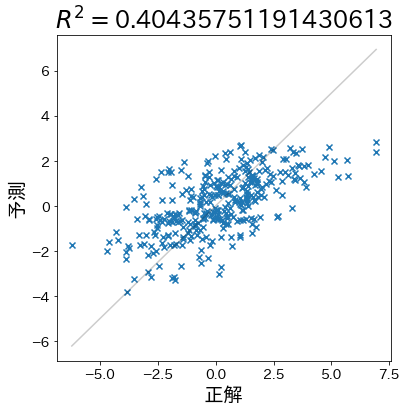
予測値と実測値の散布図（中程度のR²） — ノイズが大きいためばらつきが増し、R²は低下するが0以上を維持している。

さらに、学習の仕方が悪いと平均予測よりも悪化し \(R^2 < 0\) になります。下記は目的変数をランダムにシャッフルした例です。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
X, y = make_regression(
    n_samples=1_000,
    n_informative=3,
    n_features=20,
    effective_rank=4,
    noise=30.0,
    random_state=RANDOM_STATE,
)

train_X, test_X, train_y, test_y = train_test_split(
    X, y, test_size=0.33, random_state=RANDOM_STATE
)

train_y = np.random.permutation(train_y)
train_y = np.sin(train_y) * 10 + 1

model = RandomForestRegressor(max_depth=1, random_state=RANDOM_STATE)
model.fit(train_X, train_y)
pred_y = model.predict(test_X)

r2 = r2_score(test_y, pred_y)
y_min, y_max = np.min(test_y), np.max(test_y)

plt.figure(figsize=(6, 6))
plt.plot([y_min, y_max], [y_min, y_max], linestyle="-", color="black", alpha=0.2)
plt.scatter(test_y, pred_y, marker="x", alpha=0.6)
plt.xlabel("True")
plt.ylabel("Predicted")
plt.title(f"R^2 = {r2:.3f}")
plt.grid(alpha=0.3)
plt.show()

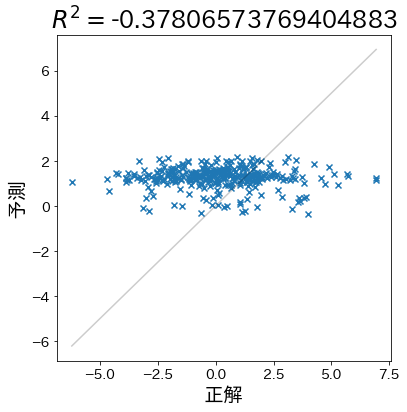
予測値と実測値の散布図（負のR²） — 目的変数をシャッフルしたため予測が破綻し、R²が負の値になっている。

負の値は「平均から予測するよりも悪い」ことを意味し、入力と目的変数の関係が崩れている可能性を示唆します。

4. 最小二乗法での性質 #

最小二乗法による単回帰モデルでは、決定係数は理論上 \(0 \le R^2 \le 1\) に収まります。ノイズを変化させながら線形回帰を 100 回繰り返した例です。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler

r2_scores: list[float] = []

for noise in np.linspace(0.0, 3.0, 100):
    X, y = make_regression(
        n_samples=500,
        n_informative=1,
        n_features=1,
        effective_rank=1,
        noise=noise,
        random_state=RANDOM_STATE,
    )

    train_X, test_X, train_y, test_y = train_test_split(
        X, y, test_size=0.33, random_state=RANDOM_STATE
    )

    model = make_pipeline(
        StandardScaler(with_mean=False),
        LinearRegression(positive=True),
    )
    model.fit(train_X, train_y)
    pred_y = model.predict(test_X)
    r2_scores.append(r2_score(test_y, pred_y))

plt.figure(figsize=(8, 4))
plt.hist(r2_scores, bins=20, color="#2563eb", alpha=0.8, edgecolor="white")
plt.xlabel("R^2 score")
plt.ylabel("Frequency")
plt.title("Distribution of R^2 across 100 noisy datasets")
plt.grid(alpha=0.3)
plt.show()

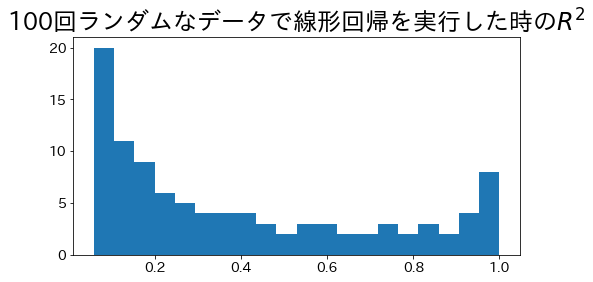
R²スコアのヒストグラム — ノイズを変化させた100回の線形回帰におけるR²の分布。ノイズが大きいほどR²は低下する。

ノイズが大きくなるほどヒストグラムが左側にシフトし、調整済み指標や交差検証の必要性が見えてきます。

5. 実務での活用と注意点 #

特徴量数の影響：特徴量を増やすほど \(R^2\) は上昇しやすいため、Adjusted R² や AIC/BIC と併用して過学習をチェックします。
目的に応じたスコア選択：平均絶対誤差（MAE）や RMSLE など、ビジネス指標と整合する評価値も併せて確認します。
サンプルが少ない場合：分散が大きくなり解釈が難しくなるため、交差検証やブートストラップで安定性を確かめます。
非線形モデリング：木系モデルやニューラルネットでは負の値が出ることも珍しくありません。リフトチャートや残差プロットと組み合わせて総合的に判断しましょう。

ノイズと R² #

ノイズ量が増えると R² がどう悪化するか確認できます。

#

まとめ #

決定係数 \(R^2\) はモデルが目的変数のばらつきをどれだけ説明できたかを表します。
平均予測より悪い場合は負の値になり、データや学習方法の見直しが必要です。
特徴量数やデータ量の影響を理解し、調整済み R² や誤差系指標と併用してモデルを評価しましょう。

自由度調整済みR² — 変数数を考慮した補正版
説明分散 — バイアス込みの分散説明
相関係数 — 線形関係の強さ